Chapter5. 陰を付ける

陰を付ける

前回はレイと物体の交差判定のみを使い，物体の輪郭を可視化した．今回は単純なシェーディングモデルに基づいた陰影処理を実装する．

beta shading
図1. (左)隠面消去のみ，(右)隠面消去＋陰影処理

Phongの反射モデル

現実の光源の複雑さ

レイトレーシング法では，全ての種類の光源と反射現象を扱うことができるわけではない．
手法の性質上，光源と反射現象を単純化して扱う必要がある．

図2. 光線追跡の難しさ

レイトレーシング法は，光が光源から我々の目に届くまでの過程を目から光源に向かって追跡しどのように見えるかを再現する手法であると以前に述べた．
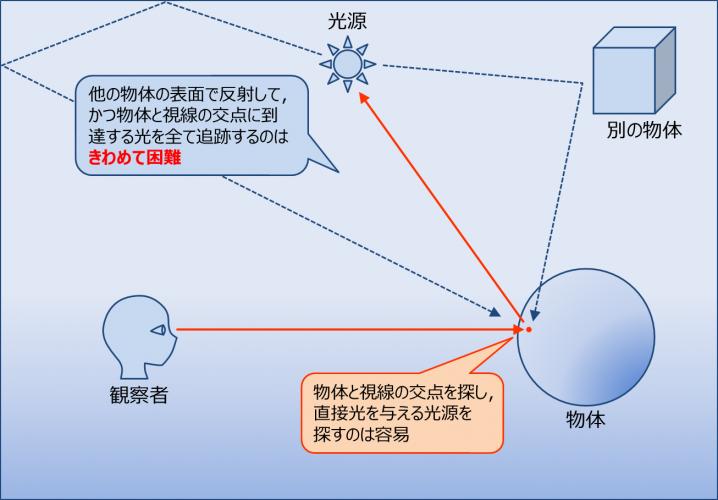
このことは，レイトレーシング法では直接光以外の光を正確に追跡することがきわめて困難であることを意味する(図2)．

レイトレーシング法では，まず視点からレイを飛ばし視線と交差する物体を探す．視線と物体の交点が見つかったら，その点に直接光を与える光源を探すのは容易である．
しかし，他の物体で何度も反射し交点に到達する全ての光を追跡することは，光源の側からも光線を追跡しない限り不可能である(双方向経路追跡法というレイトレーシング法を拡張した方法もある)．

反射現象の単純化

物体表面の反射のしかたを近似するモデルとしてPhongの反射モデルがよく使われる．
Phongの反射モデルでは，物体表面の反射を以下の三つの要素で近似する．

環境光(定数)
直接光の拡散反射光
直接光の鏡面反射光

環境光は，別の物体表面での反射を経て，物体表面にとどく光のことである（間接光ともいう）．前述のようにこれを正確にシミュレーションすることは容易ではない． Phongのモデルでは環境光とそれによる反射光の強さは定数として扱う．

また，物体表面での反射を拡散反射と鏡面反射の2種類のみとして扱う．

拡散反射：ざらざらした物体表面で光が入射点から全方位に反射する現象
鏡面反射：なめらかな物体表面で光が正反射方向に反射する現象（ハイライト）

これらの反射は直接光のみ考慮する．これらの単純化を表1にまとめる．

光源\反射現象	拡散反射	鏡面反射
表1. 光源と反射現象の単純化
直接光	考慮する	考慮する
環境光	定数として扱う

反射光の計算方法

最終的な色は環境光，拡散反射光，鏡面反射光の足し算となる(図3)．

$ R_{r} = R_{a} + R_{d} + R_{s} $

$$R_{a}$$, $$R_{d}$$, $$R_{s}$$はそれぞれ環境光，直接光の拡散反射光，直接光の鏡面反射光の放射輝度(radiance)である．

+ + =
図3. 左から，環境光，拡散反射光，鏡面反射光，それらを足しあわせたもの

次節では各々の反射光の計算方法について解説する．

環境光

環境光(ambient light)あるいは間接光(indirect light)は，光源から発せられ一回以上の反射を経て物体表面に届く光である．
ここでは物体表面に届く環境光の強度は一定とし，その反射光の放射輝度も反射面の方向によらず一定とする．

環境光の反射光の放射輝度$$R_a$$は以下のように近似する．

$ R_{a} = k_{a} I_{a} $

$$k_{a}$$は環境光反射係数(環境光を反射する度合い)であり，物体表面ごとに異なる値となる．
$$I_{a}$$は環境光の強度(intensity)であり，シーンごとに異なる値となる．

直接光の拡散反射光

拡散反射(diffuse reflection)は，光が物体表面で入射点からあらゆる方向に散乱する現象である(乱反射とも言う)．例えば紙面や石膏などは拡散反射面の例である．
散反射光は全方位に広がるため，その強さは観察者の視点位置によらない(図4)．

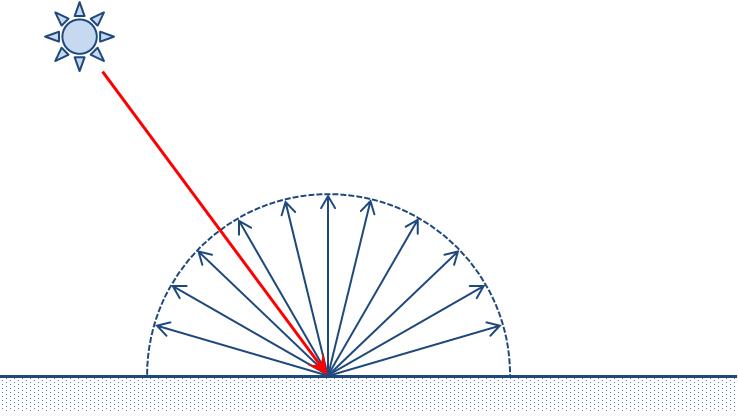
図4. 理想的な拡散反射面では全ての方向に同じ強さの光を反射する

反射光の強さはランバートの余弦則に従うことが知られている．

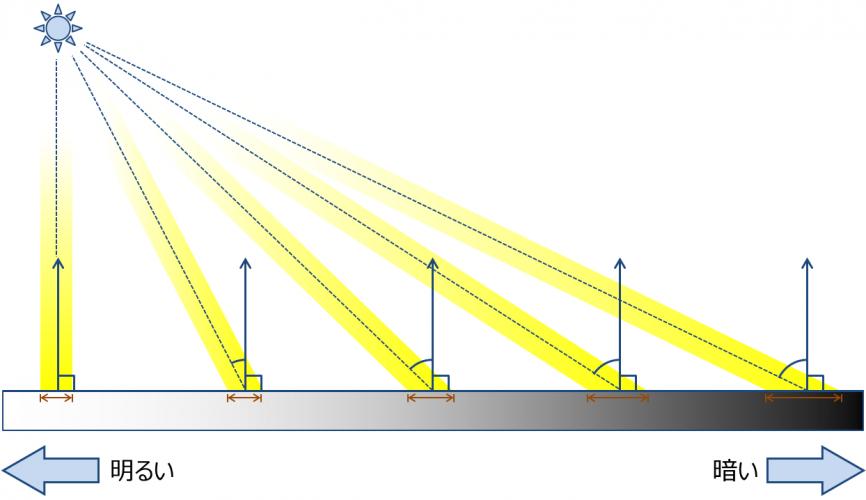
ランバートの余弦則：微小面から反射する放射強度は，面法線と光線の入射角の余弦に比例する．

この関係は光の入射角が大きくなるほど，照射される面積が大きくなり照度（単位面積あたりの光束）が小さくなることに起因する．(図5)．

図5. ランバートの余弦則

光源の強度を$$I_i$$，入射角を$$\theta$$とすると，反射される放射強度は$$R_\theta$$以下のように表現される．

$ R_\theta = I_i cos\theta \\ $

拡散反射光の放射輝度$$R_d$$は，この$$R_\theta$$に比例するため，以下のように近似することができる．

$ \begin{array} \\ R_d & = & k_{d} R_\theta \\ & = & k_{d} I_{i} cos\theta \\ \end{array} \\ $

ここで$$k_{d}$$は拡散反射係数である．

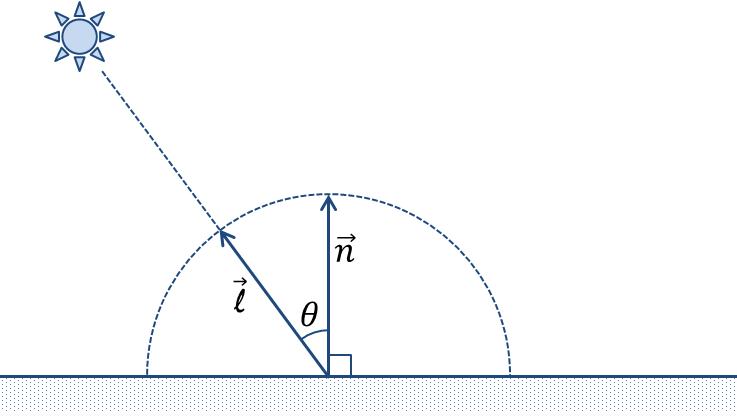
この拡散反射光の放射輝度$$R_d$$を算出するためには面法線と光線のなす入射角$$\theta$$を知る必要があるが， $$\vec{\bf n}$$を反射面の法線ベクトル，$$\vec{\bf \ell}$$を入射ベクトルとすると，上式は以下のよう表現することもできる．

$ R_d = k_{d} I_{i} \left(\vec{\bf n}\cdot\vec{\bf \ell}\right) \\ $

ただし，$$\left|\vec{\bf n}\right| = \left|\vec{\bf \ell}\right| = 1$$である必要がある．また，$$\vec{\bf \ell}$$は，(呼び名に反して)面との交点から光源へ向かうベクトルであることに注意せよ(図6)．

+ コサインが内積になった？クリックで非表示

ベクトルの内積は以下のような性質がある．

$ \vec{\bf a}\cdot\vec{\bf b} = \left|\vec{\bf a}\right|\left|\vec{\bf b}\right|cos\theta \\ $

従って，$$\left|\vec{\bf a}\right|=\left|\vec{\bf b}\right|=1$$である場合，以下が成り立つ．

$ \vec{\bf a}\cdot\vec{\bf b} = cos\theta \\ $

-クリックで非表示

図6. 法線ベクトルと入射ベクトル

法線ベクトルと入射ベクトルのなす角には注意する必要がある．
図7のように，法線ベクトルと入射ベクトルのなす角が$$\frac{\pi}{2}$$(=90°)を超えるとき，すなわち 光源が面の裏側から当たっているようなとき反射は起こらない．

実装の際は，$$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)\lt0$$のとき拡散反射光の放射輝度はゼロとして扱う．

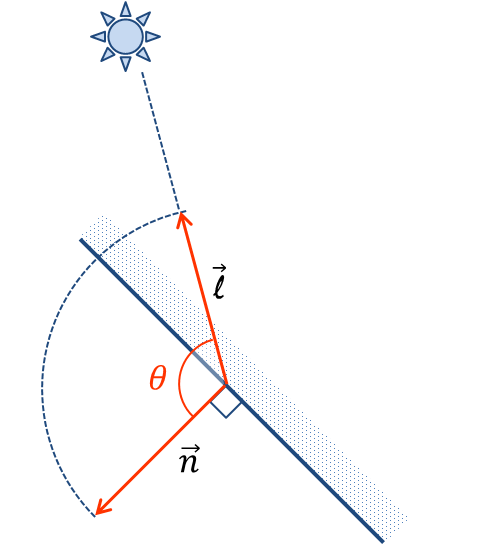
図7. 拡散反射が起こらない場合

直接光の鏡面反射光

鏡面反射(specular reflection)は金属やプラスチックなどの滑らかな表面で起こる反射である．
このような表面では光源に近い部分に明るい部分（＝ハイライト）が見える．

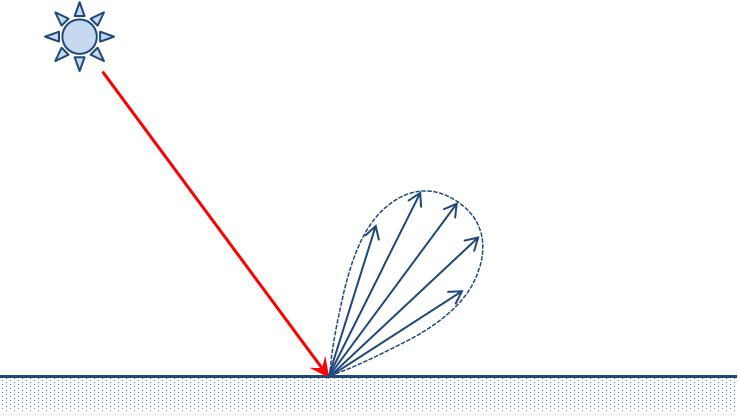
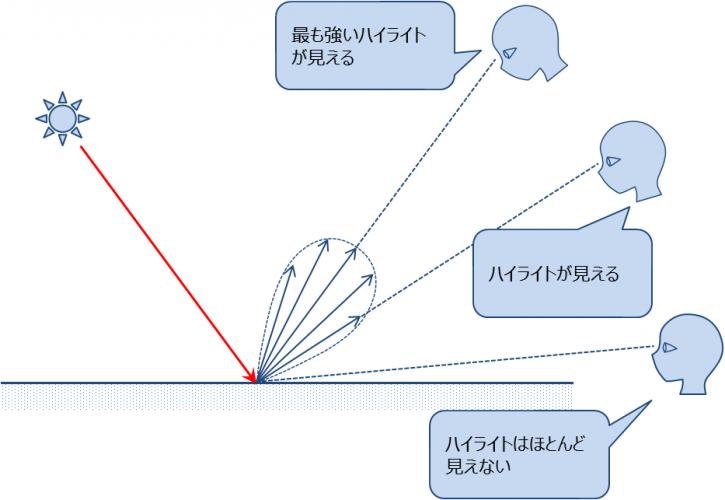
完全な鏡面では，光は入射角の正反射方向にのみ反射するが，現実的には正反射方向を中心とした範囲に広がる(図8)．

図8. 鏡面反射光は向きと広がりを持つ

鏡面反射による反射光は，拡散反射光と違い指向性を持つため，その強さは視点に依存して変化する(図9)．

図9. ハイライトの強さ

Phongの反射モデルでは鏡面反射光の放射強度$$R_s$$は以下のように近似する．

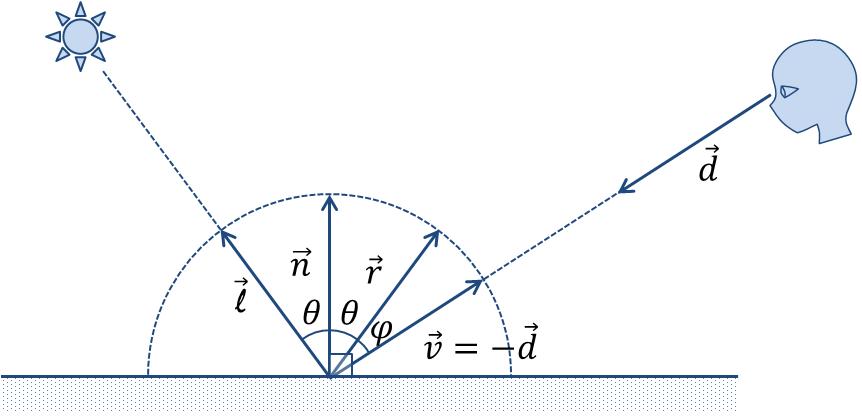
$ \begin{array}{lll} \\ R_{s} & = & k_{s}I_{i}cos^{\alpha}\phi \\ & = & k_{s}I_{i}\left(\vec{\bf v}\cdot\vec{\bf r}\right)^{\alpha} \\ \end{array}$

ここで，$$k_{s}$$は鏡面反射係数，$$I_{i}$$は入射光の強度，$$\vec{\bf v}$$は視線ベクトルの逆ベクトル，$$\vec{\bf r}$$は入射光の正反射ベクトル， $$\phi$$は$$\vec{\bf v}$$と$$\vec{\bf r}$$のなす角， $$\alpha$$は光沢度(shininess)といいハイライトの鋭さを決める係数($$1\le\alpha$$)である(図10)．また，$$\left|\vec{\bf v}\right|=\left|\vec{\bf r}\right|=1$$である．

この式では$$\vec{\bf v}$$と$$\vec{\bf r}$$のなす角$$\phi$$が小さくなるほど大きな値となる．
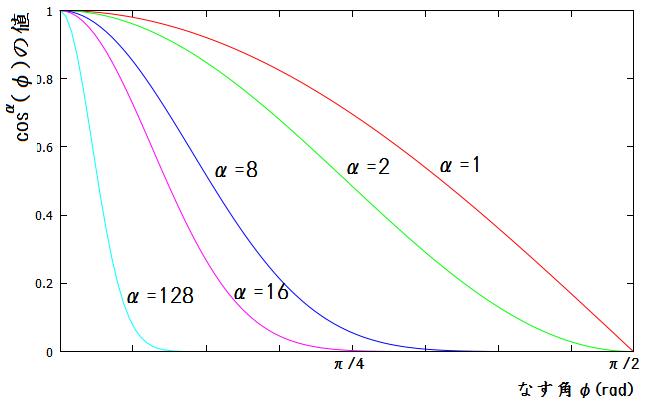
また，$$\alpha$$が大きい値になるほど$$cos^{\alpha}\phi=\left(\vec{\bf v}\cdot\vec{\bf r}\right)^{\alpha}$$の値の変化は急激になる(図11)．

図10. Phongの鏡面反射モデル

図11. 累乗された余弦関数の軌跡

法線ベクトルと入射ベクトルのなす角，および視線ベクトルの逆ベクトルと正反射ベクトルのなす角には注意する必要がある．
拡散反射光と同様に，法線ベクトルと入射ベクトルのなす角が$$\frac{\pi}{2}$$より大きいとき，すなわち$$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)\lt0$$のときは光が当たらないため鏡面反射光もゼロとなる．

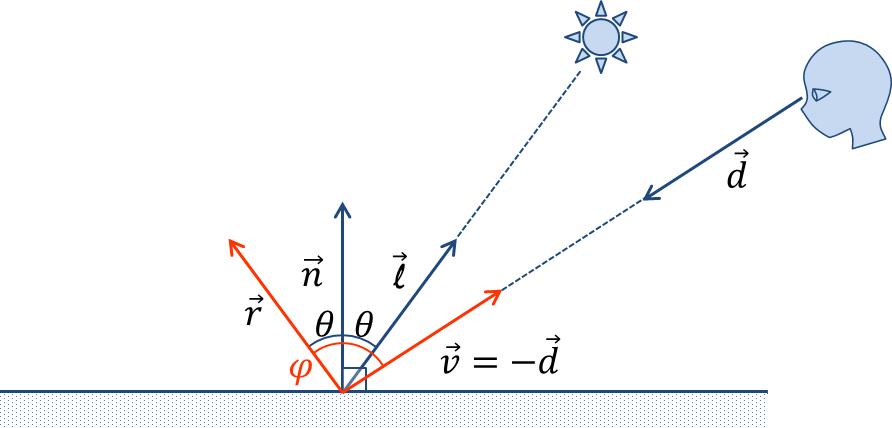
逆ベクトルと正反射ベクトルのなす角が$$\frac{\pi}{2}$$より大きいとき(図12)も鏡面反射はおこらない．

実装の際は，$$\left(\vec{\bf v}\cdot\vec{\bf r}\right)\lt0$$のときは鏡面反射光はゼロとして扱う．

図12. 鏡面反射が起こらない場合

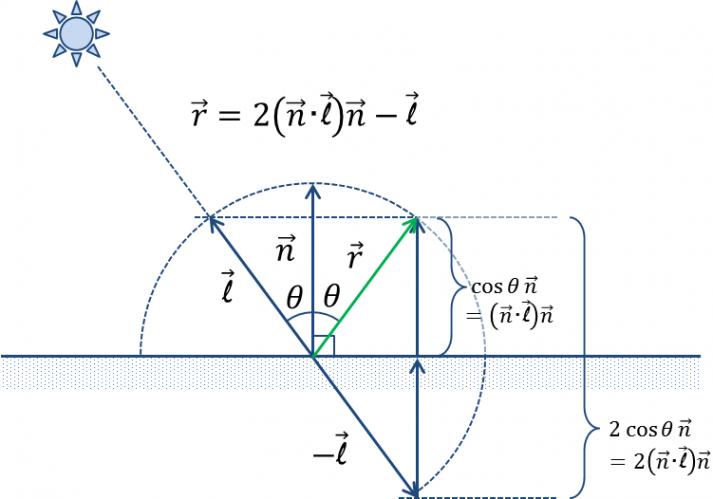
なお，正反射ベクトル$$\vec{\bf r}$$は以下のように計算することができる(図13)．

$ \vec{\bf r}=2\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)\vec{\bf n}-\vec{\bf \ell} $

図13. 正反射ベクトル

まとめ

以上の反射光に関する式を以下にまとめる．

物体表面の放射輝度

$ R_{r} = R_{a} + R_{d} + R_{s} $

$$R_{a}$$：環境光の反射光の放射輝度
$$R_{d}$$：直接光の拡散反射光の放射輝度
$$R_{s}$$：直接光の鏡面反射光の放射輝度

環境光の反射光の放射輝度

$ R_{a} = k_{a} I_{a} $

$$k_{a}$$：環境光反射係数
$$I_{a}$$：環境光の強度

直接光の拡散反射光の放射輝度

$ R_{d} = k_{d} I_{i} \left(\vec{\bf n}\cdot\vec{\bf \ell}\right) $

$$k_{d}$$：拡散反射係数
$$I_{i}$$：光源の光の強度
$$\vec{\bf n}$$：物体面の法線ベクトル($$\left|\vec{\bf n}\right|=1$$)
$$\vec{\bf \ell}$$：光の入射方向ベクトル($$\left|\vec{\bf \ell}\right|=1$$)
- 光源が始点

※ $$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)\lt0$$のとき拡散反射光の輝度はゼロである．

直接光の鏡面反射光の放射輝度

$ R_{s} = k_{s}I_{i}\left(\vec{\bf v}\cdot\vec{\bf r}\right)^{\alpha} $

$$k_{s}$$：鏡面反射係数
$$I_{i}$$：光源の光の強度
$$\vec{\bf v}$$：視線ベクトルの逆ベクトル($$\left|\vec{\bf v}\right|=1$$)
$$\vec{\bf r}$$：入射光の正反射ベクトル($$\left|\vec{\bf r}\right|=1$$)
$$\alpha$$：光沢度($$1\le\alpha$$)

※ $$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)\lt0$$あるいは$$\left(\vec{\bf v}\cdot\vec{\bf r}\right)\lt0$$のとき鏡面反射光の放射輝度はゼロである．

正反射ベクトル

$ \vec{\bf r}=2\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)\vec{\bf n}-\vec{\bf \ell} $

$$\vec{\bf n}$$：物体面の法線ベクトル($$\left|\vec{\bf n}\right|=1$$)
$$\vec{\bf \ell}$$：光の入射方向ベクトル($$\left|\vec{\bf \ell}\right|=1$$)
- 光源が始点

交点における法線ベクトルの計算

前回はレイ（半直線）と平面や球の交点を求める方法について説明した．上述のように物体表面の輝度を求めるには，物体表面の法線ベクトルが必要である．ここにレイと平面／球の交点における法線ベクトルの求め方について補足する．

平面の場合

平面の場合は，交点における法線ベクトルは面の法線ベクトルに等しい．

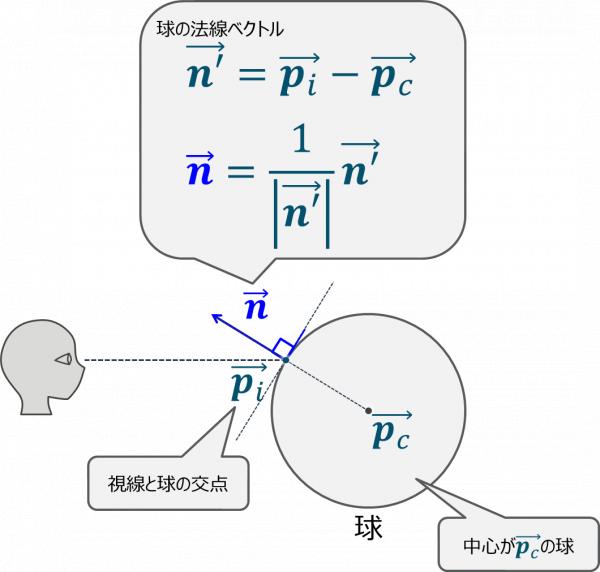
球の場合

球の場合，球の中心の位置ベクトルが$$\vec{\bf p_c}$$，交点の位置ベクトルが$$\vec{\bf p_{\cal i}}$$ならば，交点における法線ベクトルは，$$\vec{\bf n}$$は以下のようになる．

$ \vec{\bf n’} = \vec{\bf p_{\cal i}}-\vec{\bf p_c} \\ \vec{\bf n} = \frac{1}{\left|\vec{\bf n’}\right|}\vec{\bf n’} \\ $

+ 微分を用いた法線方向の算出クリックで非表示

一般に曲面がベクトル$$\vec{\bf p}$$の関数$$F(\vec{\bf p})$$で定義される場合，$$F(\vec{\bf p})$$を$$\vec{\bf p}$$で微分した導関数$$\frac{\partial F(\vec{\bf p})}{\partial \vec{\bf p}}$$に，交点位置$$\vec{\bf p_i}$$を渡すことで，法線方向ベクトルを得ることができる．

球面のベクトル方程式は，

$ \left|\vec{\bf p} – \vec{\bf c}\right|^2 = r^2 \\ $

であった．この式を整理して，以下のような関数と見なす．

$ \left|\vec{\bf p} – \vec{\bf c}\right|^2 = r^2 \\ \left|\vec{\bf p} – \vec{\bf c}\right|^2 – r^2 = 0 \\ \Leftrightarrow \\ F\left(\vec{\bf p}\right) = 0 \\ $

$$F\left(\vec{\bf p}\right)$$は以下である．

$ \begin{array}{lll} F\left(\vec{\bf p}\right) & = & \left|\vec{\bf p} – \vec{\bf c}\right|^2 – r^2 \\ & = & \left(\vec{\bf p} – \vec{\bf c}\right)\cdot\left(\vec{\bf p} – \vec{\bf c}\right) – r^2 \\ & = & \left(\vec{\bf p}\cdot\vec{\bf p}\right) – 2\left(\vec{\bf p}\cdot\vec{\bf c}\right) + \left(\vec{\bf c}\cdot\vec{\bf c}\right) – r^2 \\ \end{array} \\ $

この関数$$F\left(\vec{\bf p}\right)$$を$$\vec{\bf p}$$で微分する．ベクトルによる微分は，関数をX,Y,Zの各成分で偏微分することに等しい．物理学などに慣れていれば，これは$$\nabla$$演算子を作用させることに等しいことが分かるだろう．

$ \frac{\partial F(\vec{\bf p})}{\partial \vec{\bf p}} = \left(\begin{array} \\ \frac{\partial F(\vec{\bf p})}{\partial x} \\ \frac{\partial F(\vec{\bf p})}{\partial y} \\ \frac{\partial F(\vec{\bf p})}{\partial z} \\ \end{array}\right) = \nabla F(\vec{\bf p}) \\ $

$$F\left(\vec{\bf p}\right)$$は以下のように展開できるので，

$ \begin{array}{lll} F\left(\vec{\bf p}\right) & = & \left(\vec{\bf p}\cdot\vec{\bf p}\right) – 2\left(\vec{\bf p}\cdot\vec{\bf c}\right) + \left(\vec{\bf c}\cdot\vec{\bf c}\right) – r^2 \\ \Leftrightarrow \\ F(x,y,z) & = & x^2 + y^2 + z^2 -2 c_x x -2 c_y y -2 c_z z + {c_x}^2 + {c_y}^2 +{c_z}^2 – r^2 \\ \end{array} \\ $

導関数$$\frac{\partial F(\vec{\bf p})}{\partial \vec{\bf p}}$$は，以下のようになる．

$ \frac{\partial F(\vec{\bf p})}{\partial \vec{\bf p}} = \left(\begin{array} \\ \frac{\partial F(x,y,z)}{\partial x} \\ \frac{\partial F(x,y,z)}{\partial y} \\ \frac{\partial F(x,y,z)}{\partial z} \\ \end{array}\right) = \left(\begin{array} \\ 2 x – 2 c_x \\ 2 y – 2 c_y \\ 2 z – 2 c_z \\ \end{array}\right) \\ $

交点位置が$$\vec{\bf p_i}=(a_x , a_y , a_z)$$である場合，法線方向$$\vec{\bf n’}$$は

$ \vec{\bf n’} = \frac{\partial F(\vec{\bf p_i})}{\partial \vec{\bf p}} = \left(\begin{array} \\ \frac{\partial F(x,y,z)}{\partial x}\left|_{(x,y,z)=(a_x , a_y , a_z)}\right. \\ \frac{\partial F(x,y,z)}{\partial y}\left|_{(x,y,z)=(a_x , a_y , a_z)}\right. \\ \frac{\partial F(x,y,z)}{\partial z}\left|_{(x,y,z)=(a_x , a_y , a_z)}\right. \\ \end{array}\right) = \left(\begin{array} \\ 2 a_x – 2 c_x \\ 2 a_y – 2 c_y \\ 2 a_z – 2 c_z \\ \end{array}\right) \\ $

放射輝度の計算では，法線ベクトルは正規化されている必要があるので，$$\vec{\bf n’}$$を正規化した以下のベクトルが法線ベクトルとなる．

$ \vec{\bf n} = \frac{1}{\left|\vec{\bf n’}\right|}\vec{\bf n’} \\ $

-クリックで非表示

光源モデル

自然界には様々な光源が存在するが，本実験では特に物体表面における光線の方向を計算しやすい点光源と平行光源のみを考える(図15，図16)．

点光源

点光源は，空間中のある位置から光が全ての方向に広がる光源である．

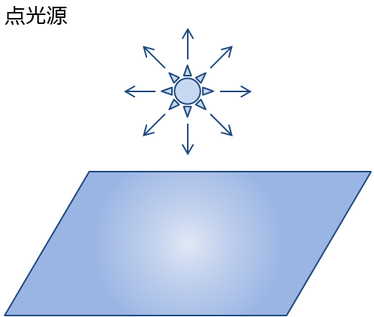
図15. 点光源

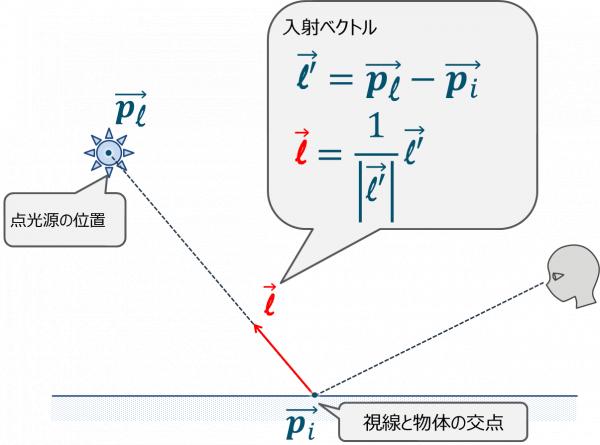
点光源の位置が$$\vec{\bf p_\ell}$$である場合，空間中の任意の点$$\vec{\bf p_i}$$における入射ベクトル$$\vec{\bf \ell}$$の計算方法は以下となる．

$ \vec{\bf \ell’} = \vec{\bf p_\ell} – \vec{\bf p_i}\\ \vec{\bf \ell} = \frac{1}{\left|\vec{\bf \ell’}\right|}\vec{\bf \ell’} \\ $

平行光源

平行光源は，空間中のあらゆる位置で同じ方向をもつ光源である．

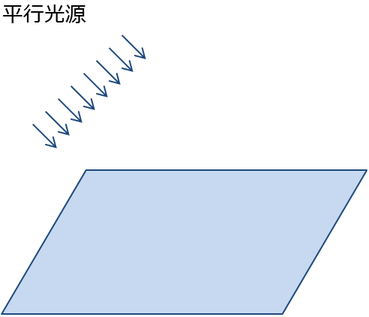
図16. 平行光源

平行光源の方向ベクトルが$$\vec{\bf d_{\ell}}$$である場合，空間中の任意の点$$\vec{\bf p_i}$$における入射ベクトル$$\vec{\bf \ell}$$の計算方法は以下となる．

$ \vec{\bf \ell’} = -\vec{\bf d_{\ell}} \\ \vec{\bf \ell} = \frac{1}{\left|\vec{\bf \ell’}\right|}\vec{\bf \ell’} \\ $

式中に$$\vec{\bf p_i}$$が登場しないことからも分かるとおり，平行光源からの光はいかなる位置においても同じ方向である．

光の減衰

実際の光は，光源からの距離の二乗に反比例して弱くなる（逆二乗の法則）が，簡単化のため本実験では光の減衰は考慮しない．

(実装の面から言うと逆二乗の法則を考慮してしまうとシーンがきわめて暗くなる．これは直接光による照明しか考慮していないためである．現実には我々の目に入る物体表面の反射光は，間接光による反射光が大きな割合を占めている．)

課題

課題2-1. 最初の陰影処理（拡散反射光のみ）

「課題1-7 レイと球の交差判定」の実装に，拡散反射による陰影処理を追加せよ．このスケッチはDiffuseOnlyという名前で保存すること．

このスケッチでは，Phoneの反射モデルのうち考慮するのは拡散反射光のみであるため，物体表面の放射輝度$$R_r$$は以下のように単純化される．

$ R_{r} = R_{d} $

$$R_{d}$$：直接光の拡散反射光の放射輝度

また，拡散反射係数と光源の光の強度はともに$$1$$として扱う．したがって，直接光の拡散反射光の放射輝度$$R_d$$は以下のように単純化される．

$ R_{d} = \left(\vec{\bf n}\cdot\vec{\bf \ell}\right) $

$$\vec{\bf n}$$：物体面の法線ベクトル($$\left|\vec{\bf n}\right|=1$$)
$$\vec{\bf \ell}$$：光の入射方向ベクトル($$\left|\vec{\bf \ell}\right|=1$$)

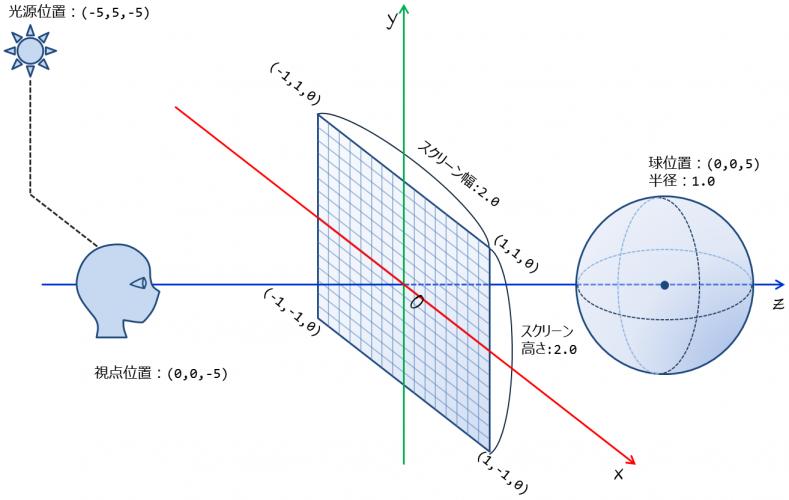
シーンは，「シーン設定」と同じだが，点光源（光源位置$$\vec{\bf p_{\ell}}=(-5,5,-5)$$）を追加する(図18)．

視点位置
- $$\vec{\bf p_{\cal e}}=(0,0,-5)$$
スクリーン位置
- 左上$$(-1,1,0)$$, 右上$$(1,1,0)$$, 右下$$(1,-1,0)$$, 左下$$(-1,-1,0)$$
球
- 中心位置$$\vec{\bf p_{\cal c}}=(0,0,5)$$
- 半径$$1.0$$
光源位置
- $$\vec{\bf p_{\ell}}=(-5,5,-5)$$
背景色
- 前回は背景(球と交差しない場合)の色は$$RGB=(0,0,255)$$としたが好きな色に変えてよい．
- 以降の出力例では$$RGB=(100, 149, 237)$$(cornflowerblue)である．

図18. シーン設定

画像サイズは幅512ピクセル，高さ512ピクセルとせよ．

生成画像は図19のようになる．

図19. DiffseOnlyの生成画像

ヒント１

+ クリックで表示クリックで非表示

入射ベクトルと法線ベクトルの内積を画素値として使う($$[0,1]\rightarrow[0,255]$$のマッピングは必要)．

-クリックで非表示

ヒント２

+ ソースを日本語で書き下したものクリックで非表示

判別式$$D=0$$のとき
- $$t=\frac{-B}{2A}$$
判別式$$D>0$$のとき
- $$t=\frac{-B+\sqrt{D}}{2A},\frac{-B-\sqrt{D}}{2A}$$
- 二つの$$t$$のうち，値が正でかつ小さい方を$$t$$とする．
$$t\gt0$$のとき
1. 交点位置$$\vec{\bf p_{\cal i}}$$を計算する．
  - $$\vec{\bf p_{\cal i}}=\vec{\bf p_{\cal e}}+t\vec{\bf d_{\cal e}}$$
2. 入射ベクトル$$\vec{\bf \ell}$$を計算する．
  - $$\vec{\bf \ell}=\vec{\bf p_{\ell}}-\vec{\bf p_{\cal i}}$$
  - 正規化が必要であることに注意せよ．
3. 法線ベクトル$$\vec{\bf n}$$を計算する．
  - $$\vec{\bf n}=\vec{\bf p_{\cal i}}-\vec{\bf p_{\cal c}}$$
  - 正規化が必要であることに注意せよ．
4. 内積$$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)$$を計算する．
5. 内積$$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)$$の値を$$[0,1]$$の範囲に切り詰める．
  - 内積なので値の範囲は$$[-1,1]$$である．
  - 内積が0以下のときは光が当たっていないので0として扱う．
6. 色を出力する．
  - $$gray=255\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)$$
    - 計算誤差などにより$$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)$$が1.0を超えてしまうと不正な画素値となってしまうため，$$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)$$の値が$$[0,1]$$の範囲に収まるように制限する必要がある．
  - $$RGB=(gray, gray, gray)$$を出力する．
$$t\gt0$$以外のとき
- 背景色を出力する(たとえば$$RGB=(100, 149, 237)$$)．

-クリックで非表示

ヒント３

+ ソース穴埋めクリックで非表示

ソース穴埋め

-クリックで非表示

課題2-2. 最初の陰影処理（環境光，拡散反射光，鏡面反射光）

「課題2-1. 最初の陰影処理（拡散反射光のみ）」の実装に，環境光と鏡面反射による陰影処理を追加せよ．シーン設定は課題2-1に準じる．
このスケッチはSimpleShadingという名前で保存すること．

ライティングに関わるパラメータは以下とせよ．

環境光反射係数
- $$k_{a}=0.01$$
拡散反射係数
- $$k_{d}=0.69$$
鏡面反射係数
- $$k_{s}=0.3$$
光沢度
- $$\alpha=8$$
環境光の強度
- $$I_{a}=0.1$$
光源の光の強度
- $$I_{i}=1.0$$

画像サイズは幅512ピクセル，高さ512ピクセルとせよ．

生成画像は図20のようになる．

図20. SimpleShadingの生成画像

ヒント１

+ ソースを日本語で書き下したものクリックで非表示

交差がある場合($$t\gt0$$)の場合の処理は以下のようになる．

環境光の反射光の放射輝度$$R_{a}$$を計算する．
- $$R_{a}=k_{a}I_{a}$$
交点位置$$\vec{\bf p_{\cal i}}$$を計算する．
入射ベクトル$$\vec{\bf \ell}$$を計算する．
法線ベクトル$$\vec{\bf n}$$を計算する．
内積$$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)$$を計算する．
内積$$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)$$の値を$$[0,1]$$の範囲に制限する．
直接光の拡散反射光の放射輝度$$R_{d}$$を計算する．
- $$R_{d}=k_{d}I_{i}\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)$$
$$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)\gt0$$のとき
1. 正反射ベクトル$$\vec{\bf r}$$を計算する．
  - $$\vec{\bf r}=2\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)\vec{\bf n}-\vec{\bf \ell}$$
2. 視線ベクトルの逆ベクトル$$\vec{\bf v}$$を計算する．
  - $$\vec{\bf v}=-\vec{\bf d_{\cal e}}$$
  - 正規化が必要であることに注意せよ．
3. 内積$$\left(\vec{\bf v}\cdot\vec{\bf r}\right)$$を計算する．
4. 内積$$\left(\vec{\bf v}\cdot\vec{\bf r}\right)$$の値を$$[0,1]$$の範囲に制限する．
5. 直接光の鏡面反射光の放射輝度$$R{s}$$を計算する．
  - $$R_{s}=k_{s}I_{i}\left(\vec{\bf v}\cdot\vec{\bf r}\right)^{\alpha}$$
$$\left(\vec{\bf n}\cdot\vec{\bf \ell}\right)\gt0$$以外のとき
1. 直接光の鏡面反射光の放射輝度$$R_{s}$$はゼロとする．
反射光の放射輝度$$R_{r}$$を計算する．
- $$R_{r}=R_{a}+R_{d}+R_{s}$$
色を出力する．
- $$gray=255R_{r}$$
  - 計算誤差などにより$$R_r$$が1.0を超えてしまうと不正な画素値となってしまうため，$$R_r$$の値が$$[0,1]$$の範囲に収まるように制限する必要がある．
- $$RGB=({\rm gray}, {\rm gray}, {\rm gray})$$を出力する．

-クリックで非表示

ヒント２

+ ソース穴埋めクリックで非表示

ソース穴埋め

-クリックで非表示

The Textbook of RayTracing @TDU

東京電機大学工学部第二部情報通信工学実験　グラフィックス応用テキスト