Chapter3. レイと物体の交差判定

交差判定について

レイトレーシング法を用いるにはレイ（半直線）と物体の交点を求める必要がある．

現実の物体の形状はきわめて複雑であり，レイとの交点を求めることはおろか，その形状をプログラム中で利用できるように記述することも容易ではない．

そこで，ここでは交点を求める物体として球と平面(無限平面)を扱う．これらの物体とレイの交点を求めるのは比較的容易である．

さまざまな物体の方程式

ベクトル方程式について

曲面や点の位置を示すのにベクトル方程式を用いると便利な場合がある．

ベクトル方程式とは，等式の中にベクトルが出現する方程式である．
もっとも簡単なベクトル方程式は以下のようなものである．

$$\vec{\bf a}=\vec{\bf b}$$

この方程式はベクトル$$\vec{\bf a}$$と$$\vec{\bf b}$$が，同じ向きと大きさをもつことを意味する．

ベクトル方程式で注意するべきことは，両辺ともスカラーであるか，両辺ともベクトルである方程式しか意味を持たないということである（スカラーとはベクトルに対して単一の値のみを持つ量を意味する．例えば，ベクトルの成分はスカラーである）．
たとえば，以下のような方程式の左辺がベクトル量で左辺がスカラー量であるような方程式は成立し得ない．

$ \left(\begin{array} \\ 5 \\ 3 \\ 8 \end{array}\right)=42 \ldots ? $

ベクトルに対する演算には，結果がベクトルになる演算（実数倍，加算，減算，外積）と，結果がスカラーになる演算（ベクトルのノルム，内積など）がある．
以降でベクトル方程式をいろいろと変形する部分があるため，この点に注意すること．

本節の残りの部分では，ベクトル方程式を用いてレイ（半直線），球，平面を表現する．
ただし，わかりやすさのため初等数学で用いる解析表示も併記する．

レイ（半直線）の方程式

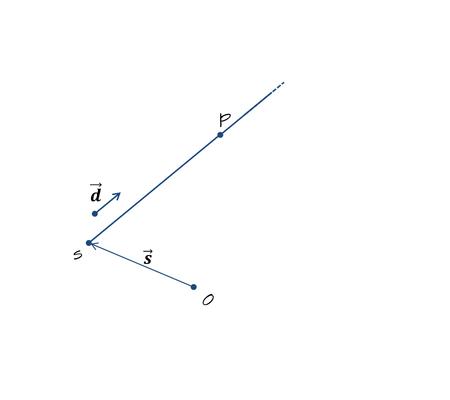
レイ（半直線）は直線と似ているが，始点を持ち始点から無限に伸びる直線である(図1)．レイは始点$$s$$と方向ベクトル$$\vec{\bf d}$$で定義される．

レイの方程式は媒介変数$$t(t \ge 0)$$を用いて以下のように表すことができる．

$ \left\{\begin{array} \\ x = s_{x} + td_{x} \\ y = s_{y} + td_{y} \\ z = s_{z} + td_{z} \\ \end{array}\right. $

(添え字つきの$$s$$,$$d$$はそれぞれ始点の位置ベクトルと方向ベクトルの成分である．)
(直線の方程式は，媒介変数を消去して$$\frac{x-s_{x}}{d_{x}}=\frac{y-s_{y}}{d_{y}}=\frac{z-s_{z}}{d_{z}}$$と表す場合もある．)

ベクトル方程式で表すと以下のようになる．

$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d}$$

($$\vec{\bf s}$$は点$$s$$の位置ベクトルである．)

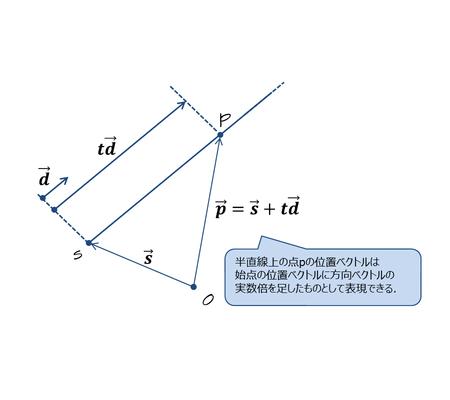
文章で書けば，半直線上の点$$p$$の位置ベクトルは始点の位置ベクトルに方向ベクトルの実数倍を足したものとして表現できる，ということである(図2)．

平面の方程式

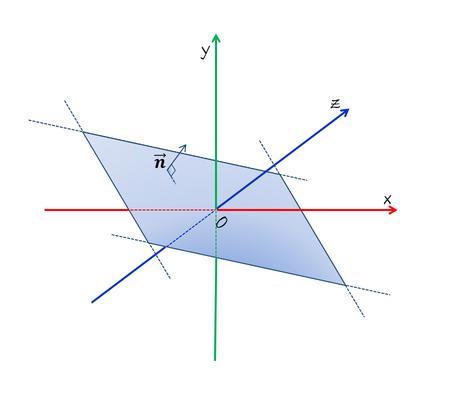
原点を通る，平面の方程式は以下である．

$ax+by+cy=0$

これは$$a,b,c$$を法線ベクトル(平面に直交するベクトル)の成分に持つ平面である．

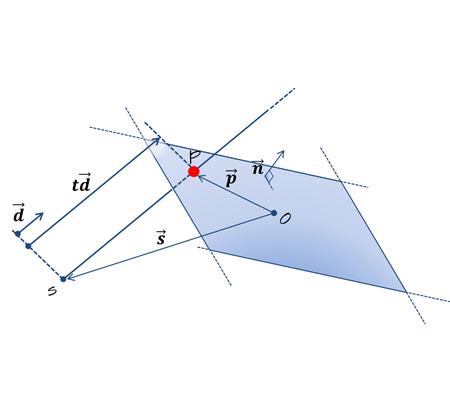
この式は以下のように主張している．

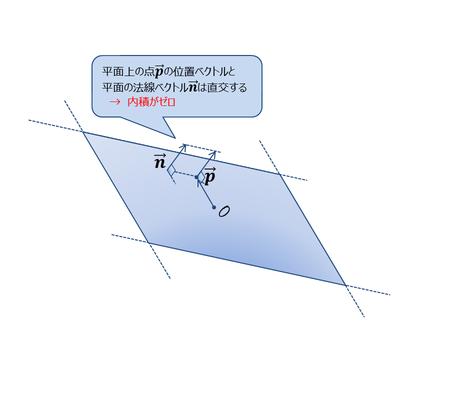
この(曲)面に属する点$$\vec{\bf p}=(x,y,z)$$と法線ベクトル$$\vec{\bf n}=(a,b,c)$$の内積は0である(図4)．

このことをベクトル方程式で表現すると以下のようになる．

$\left(\vec{\bf p}\cdot\vec{\bf n}\right)=0$

球の方程式

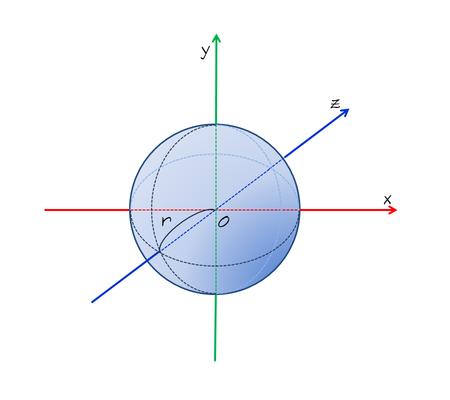
原点を中心とする，球の方程式は以下である．

$x^{2}+y^{2}+z^{2}=r^{2}$

この式は以下のように主張している．

この曲面上の点$$p=(x,y,z)$$と原点の距離は$$r$$である．

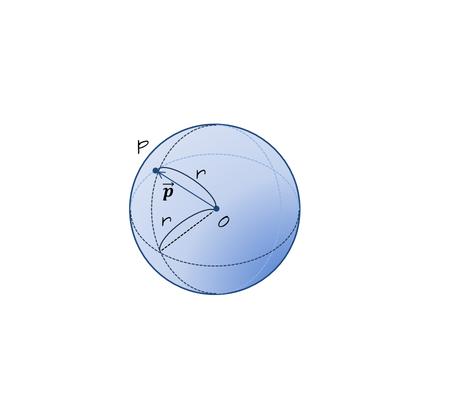
言い換えると

この曲面上の点$$p$$の位置ベクトル$$\vec{\bf p}=(x,y,z)$$のノルム(長さ)は$$r$$である(図6)．

このことをベクトル方程式で表現すると以下のようになる．

$\left|\vec{\bf p}\right|=r$

のちの計算でこの式を用いる場合，ベクトルのノルムには平方根が入るため両辺を二乗する場合がある．

$\left|\vec{\bf p}\right|^{2}=r^{2}$

レイと物体の交差判定

実際にレイと物体の交差判定を行うには上述した方程式を連立しレイの方程式中のtの値を調べればよい．

レイと平面の交差判定

レイのベクトル方程式：$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d} \ldots (1)$$
平面のベクトル方程式：$$\left(\vec{\bf p}\cdot\vec{\bf n}\right)=0 \ldots (2)$$

式(2)に式(1)を代入する(内積は分配法則が成り立つことに注意せよ)．

$ \left(\left(\vec{\bf s}+t\vec{\bf d}\right)\cdot\vec{\bf n}\right)=0 \ldots (3) $

式(3)を$$t$$について解く．

$\begin{array} \\ \left(\left(\vec{\bf s}+t\vec{\bf d}\right)\cdot\vec{\bf n}\right)=0 \\ \left(\vec{\bf s}\cdot\vec{\bf n}\right)+t\left(\vec{\bf d}\cdot\vec{\bf n}\right)=0 \\ t\left(\vec{\bf d}\cdot\vec{\bf n}\right)=-\left(\vec{\bf s}\cdot\vec{\bf n}\right) \\ t=-\frac{\left(\vec{\bf s}\cdot\vec{\bf n}\right)}{\left(\vec{\bf d}\cdot\vec{\bf n}\right)} \end{array}$

tの値の解釈

$$t$$の値は以下のように解釈できる．

まず，$$t$$の分母がゼロの場合，すなわち$$\left(\vec{\bf d}\cdot\vec{\bf n}\right)=0$$のときレイと平面は交点を持たない．

二つのベクトルの内積がゼロということは，それらのベクトルが直交しているということである（レイの方向ベクトル$$\vec{\bf d}$$と平面の法線ベクトル$$\vec{\bf n}$$が直交しているならば交点は持たない）．

それ以外の場合は以下である．

$$t \gt 0$$のとき：レイは平面と交点を持つ．交点は$$\vec{\bf s}+t\vec{\bf d}$$である．
$$t = 0$$のとき：レイの始点は平面上にある．
$$t \lt 0$$のとき：平面はレイの法線ベクトルの逆方向，すなわちレイの始点よりも後ろにある．したがって交点を持たない．

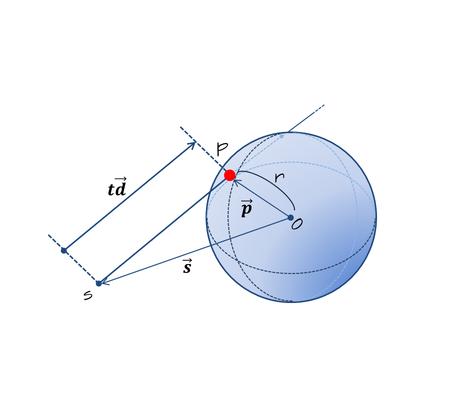
レイと球の交差判定

レイのベクトル方程式：$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d} \ldots (1)$$
球のベクトル方程式：$$\left|\vec{\bf p}\right|^{2}=r^{2} \ldots (2)$$

式(2)に式(1)を代入する．

$ \left|\vec{\bf s}+t\vec{\bf d}\right|^{2}=r^{2} \ldots (3) $

式(3)を$$t$$について解く（同じベクトル自身との内積は，そのベクトルのノルム（長さ）の二乗となることに注意せよ）．

$\begin{array} \\ \left|\vec{\bf s}+t\vec{\bf d}\right|^{2}=r^{2} \\ \left(\vec{\bf s}+t\vec{\bf d}\right)\cdot\left(\vec{\bf s}+t\vec{\bf d}\right)=r^{2} \\ \left(\vec{\bf s}\cdot\vec{\bf s}\right) + 2\left(\vec{\bf s}\cdot\vec{\bf d}\right)t + \left(\vec{\bf d}\cdot\vec{\bf d}\right)t^{2} = r^{2} \\ |\vec{\bf s}|^{2} + 2\left(\vec{\bf s}\cdot\vec{\bf d}\right)t + |\vec{\bf d}|^{2}t^{2} = r^{2} \\ |\vec{\bf d}|^{2}t^{2} + 2\left(\vec{\bf s}\cdot\vec{\bf d}\right)t + |\vec{\bf s}|^{2} = r^{2} \\ |\vec{\bf d}|^{2}t^{2} + 2\left(\vec{\bf s}\cdot\vec{\bf d}\right)t + |\vec{\bf s}|^{2} – r^{2} = 0 \ldots (4)\\ \end{array}$

式(4)はtに関する二次方程式となっている．すなわち，$$A,B,C$$を以下のようにおくと，

$ \begin{array}{lll} A & = & |\vec{\bf d}|^{2} \\ B & = & 2\left(\vec{\bf s}\cdot\vec{\bf d}\right) \\ C & = & |\vec{\bf s}|^{2}-r^{2} \\ \end{array} $

式(4)は以下の形となっている．

$ At^{2} + Bt + C = 0 \ldots (4)’ $

したがってtの根は以下である．

$ t = \frac{-B\pm\sqrt{B^{2}-4AC}}{2A} $

※ この公式に上述の$$A,B,C$$の値を当てはめてさらに展開する必要はない.
なぜなら、これらの式を計算機上で計算する場合は$$A,B,C$$を変数として用意して$$t$$の計算を行えばよいためである.

tの値の解釈

tの値は以下のように解釈できる．

まず，判別式$$D=B^{2}-4AC$$のとき$$t$$は実根を持たない．この場合は，レイと球が交差しないことを意味する．

$$D = 0$$のとき，レイは球とただ一つの交点を持つ．
$$D \gt 0$$のとき，レイは球と二つの交点を持つ．

$$t \gt 0$$のとき：レイは球と交点を持つ．交点は$$\vec{\bf s}+t\vec{\bf d}$$である．
$$t = 0$$のとき：レイの始点は球面上にある．
$$t \lt 0$$のとき：球はレイの法線ベクトルの逆方向，すなわちレイの始点よりも後ろにある．したがって交点を持たない．

課題

課題1-4 任意の点を通る平面とレイの交点

(作業時間目安：15分)

平面の方程式は以下であると前節で述べた．

$ ax+by+cy=0 \\ \Leftrightarrow \\ \left(\vec{\bf p}\cdot\vec{\bf n}\right)=0 $

これは平面が原点を通る場合の方程式である．一般に任意の点$$\vec{\bf p_c}=(c_x,c_y,c_z)$$を通る平面の方程式は以下のように表される．

$ a(x-c_x)+b(y-c_y)+c(z-c_z)=0 \\ $

ベクトル方程式として表現すると，

$ \left(\vec{\bf p}-\vec{\bf p_c}\right)\cdot\vec{\bf n}=0 \ldots (1) \\ $

となる．

式(1)とレイの方程式$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d} \ldots (2)$$を連立させ，tの一般解を求めよ．

課題1-5 任意の点を中心とする球とレイの交点

(作業時間目安：15分)

球の方程式は以下であると前節で述べた．

$ x^{2}+y^{2}+z^{2}=r^{2} \\ \Leftrightarrow \\ \left|\vec{\bf p}\right|^{2}=r^{2} \\ $

これは球が原点を中心とする場合の方程式である．一般に任意の点$$\vec{\bf p_c}=(c_x,c_y,c_z)$$を中心とする球の方程式は以下のように表される．

$ (x-c_x)^{2}+(y-c_y)^{2}+(z-c_z)^{2}=r^{2} \\ $

ベクトル方程式として表現すると，

$ \left|\vec{\bf p}-\vec{\bf p_c}\right|^{2}=r^{2} \ldots (1) \\ $

となる．

式(1)とレイの方程式$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d} \ldots (2)$$を連立させ，tの一般解を求めよ．

The Textbook of RayTracing @TDU

東京電機大学工学部第二部情報通信工学実験　グラフィックス応用テキスト