参考文献: 千葉 則茂,村岡 一信(著)「CによるCGレイトレーシング」(サイエンス社)
光の屈折
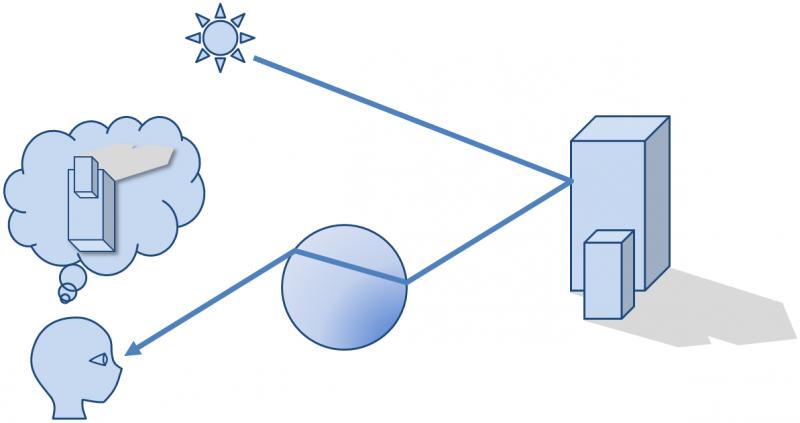
水やグラス,ビー玉など,光が透過する物質では別の物体との境界(媒質の境界)において光が直進せず屈折する(図1).
完全鏡面反射と同様に,光が透過する物体を見ているとき,観察される色は物体そのものの色ではなく 物体を通過して届いた別の物体の色である(図2).
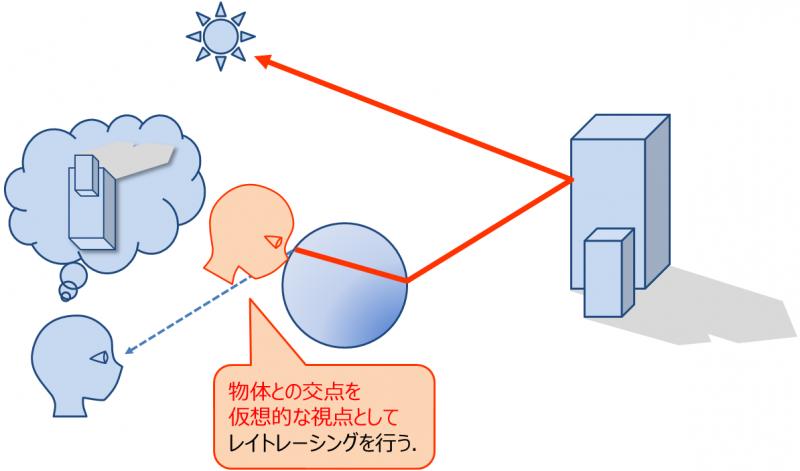
これをレイトレーシング法で再現するには,完全鏡面反射を実装したときと同様に, 物体表面の色を決める処理の中で,視線と物体の交点を仮想的な視点としてレイトレーシングを行えばよい(図3).
屈折方向および光の反射量・透過量には法則が存在する.次節ではそれらについて解説する.
光の屈折に関する物理法則
透過と完全鏡面反射の関係
光が透過する物体では,必ず完全鏡面反射も起こる.前章で扱った完全鏡面反射は物体が光を透過しない 透過現象の特別な場合である.
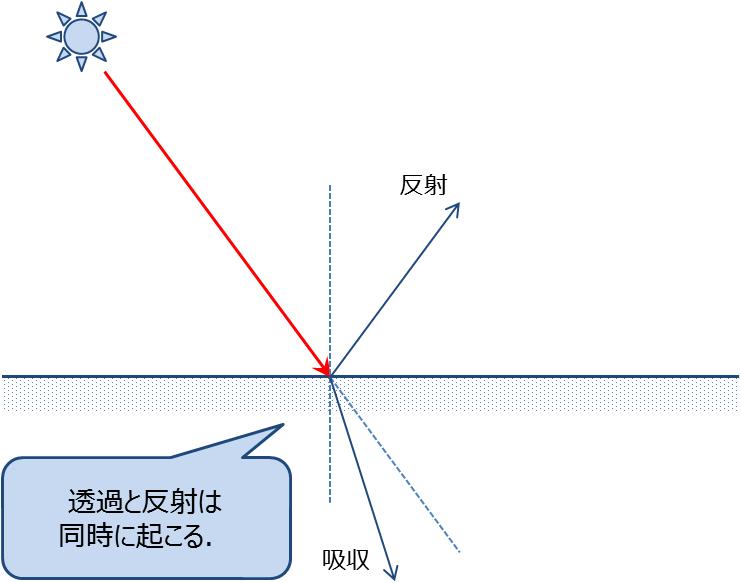
つまり,光が透過する物体の表面に光が入射すると,光の一部が物体内部に透過し,残りが反射する(図4).
反射する場合は光の入射角の正反射方向に反射するのであるが,透過する場合には物質の屈折率に依存して屈折方向が決まる. この関係を表すのがスネルの法則である.
また,どれだけの割合の光が透過し,どれだけの割合の光が反射されるのかは物体の屈折率,入射角,屈折角に応じて決まる.この関係を表すのがフレネルの公式である.
屈折方向の計算~スネルの法則
スネルの法則は,光が屈折する際の屈折方向に関する法則である.
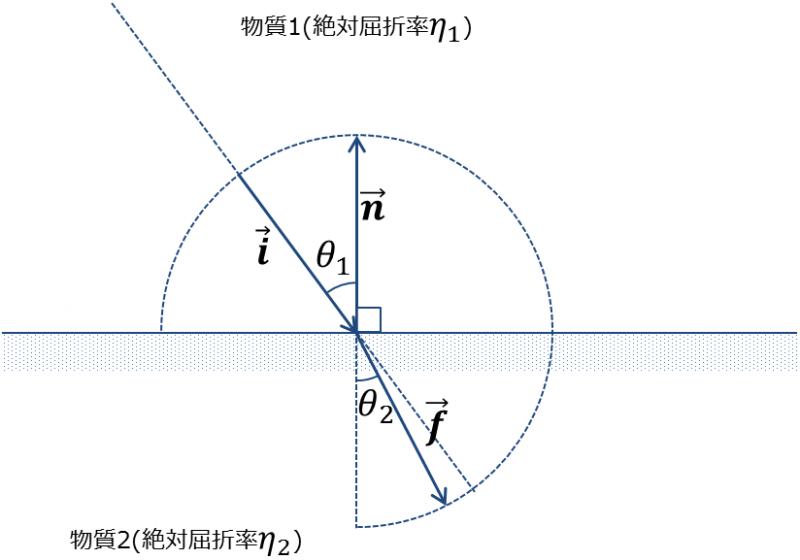
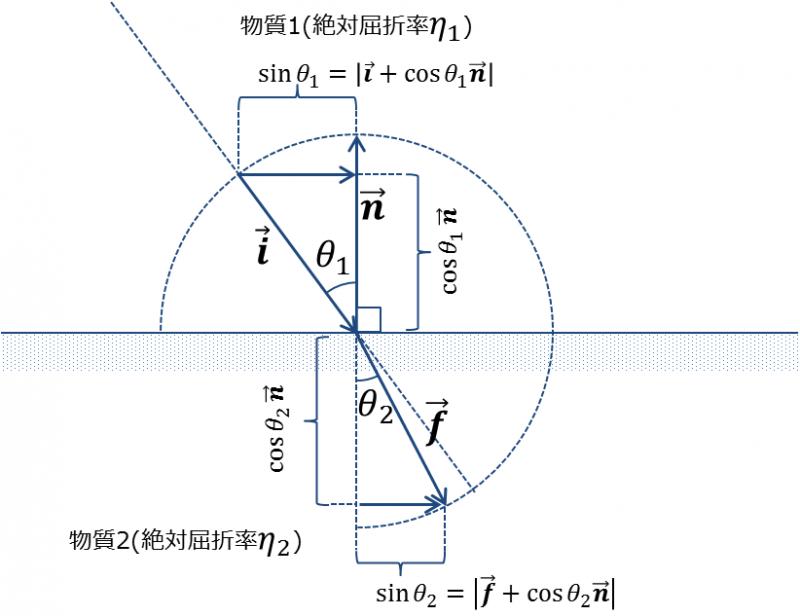
絶対屈折率$$\eta_{1}$$の物質1から,絶対屈折率$$\eta_{2}$$の物質へ光が入射するとき, 入射角$$\theta_{1}$$と屈折角$$\theta_{2}$$には以下の関係が成立する(図5).
実際に屈折角を計算する場合には,入射ベクトル$$\vec{\bf i}$$,法線ベクトル$$\vec{\bf n}$$と物質1,2の 絶対屈折率$$\eta_{1},\eta_{2}$$から,屈折ベクトル$$\vec{\bf f}$$を求めることになる(図6).
屈折ベクトル$$\vec{\bf f}$$は以下のように計算できる.
導出過程を以下に示す.
(全て単位ベクトルである.また,入射ベクトル$$\vec{\bf i}$$と呼んでいるが,今までの扱いと違い,入射点に向かうベクトルであることに注意せよ.)
図6より,$$sin\theta_{1}$$,$$sin\theta_{2}$$はそれぞれ以下であることが分かる.
これらを式(1)に当てはめると.
ベクトル$$\vec{\bf i}+cos\theta_{1}\vec{\bf n}$$と$$\vec{\bf f}+cos\theta_{2}\vec{\bf n}$$は長さが違うだけで同じ方向を持った ベクトルである(図7の面と平行な右向きのベクトル).
従ってこの式はベクトル方程式として書き表すことができる.
この式を$$\vec{\bf f}$$について整理すると,
$$cos\theta_{2}$$が未知であるが,式(1)を変形することで$$cos\theta_{2}$$を得ることができる.すなわち,
$$\pm$$が付いているが,$$cos\theta_{2}$$が負の場合,つまり屈折角が$$\frac{\pi}{2}$$(=90°)を超えることはあり得ないので,
式(7)を式(6)に代入すると,
結局,屈折ベクトル$$\vec{\bf f}$$は,
となる.
完全鏡面反射光と屈折光の比率~フレネルの公式
フレネルの公式は,完全鏡面反射光と屈折光の比率を表す式である.
物質の絶対屈折率が$$\eta_{1},\eta_{2}$$,入射角が$$\theta_{1}$$,屈折角が$$\theta_{2}$$である時, 光の完全鏡面反射率$$c_{r}$$と透過率$$c_{t}$$は以下のようになる.
$$\rho_{\parallel}$$,$$\rho_{\perp}$$は,それぞれp偏光反射率,s偏光反射率で,以下のように定義される.
(p偏光s偏光とは光が物質の境界面に進入する際の偏光成分であるが,実装の際は単に上記の式を使えばよいため,ここではこれ以上の解説はしない. 気になる者は調べてみると良い.)
反射光の計算式
以上の屈折に関する物理法則から反射光の放射輝度の計算式は以下のようになる.
屈折光を計算するための仮想的な視点位置と視線方向は以下のようになる.
- 仮想的な視点の位置
- 物体と(大元の)視線との交点$$\vec{\bf p_{\cal i}}$$
- 仮想的な視点の視線方向
- スネルの法則に基づいた屈折方向$$\vec{\bf f_{\cal e}}$$
- $$\vec{\bf f_{\cal e}} = \frac{\eta_{1}}{\eta_{2}}\left(\vec{\bf d_{\cal e}}-\left(\sqrt{\left(\frac{\eta_{2}}{\eta_{1}}\right)^{2}-\left(1-cos^{2}\theta_{1}\right)}-cos\theta_{1}\right)\vec{\bf n}\right)$$
- $$\vec{\bf d_{\cal e}}$$:(大元の)視線ベクトル(正規化する必要がある)
- $$\vec{\bf n}$$:面の法線ベクトル
反射光の計算式は完全鏡面反射の場合と同じである.
- $$R_{a}$$:環境光の反射光の放射輝度
- $$R_{di}$$:i番目の光源からの直接光の拡散反射光の放射輝度
- $$R_{si}$$:i番目の光源からの直接光の鏡面反射光の放射輝度
- $$R_{f}$$:完全鏡面反射光・屈折光の放射輝度
完全鏡面反射光・屈折光の放射輝度$$L_{f}$$を以下のように変更する.
- $$k_{f}$$:完全鏡面反射・屈折係数
- $$c_{r}$$:完全鏡面反射率
- $$c_{t}$$:透過率
- $$R_{re}$$:視線ベクトルの正反射方向$$\vec{\bf r_{\cal e}}$$方向で得られる放射輝度
- $$R_{fe}$$:$$\vec{\bf f_{\cal e}}$$方向で得られる放射輝度
光の屈折の実装
仮想的な視点の位置と方向
「シャドウレイ」と同様に始点位置に注意する.
(大元の)視線ベクトルと物体の交点をそのままレイの始点として使用するとうまくいかない(説明省略).
Materialクラス,Sceneクラスの変更
前節の屈折光の対応のため,Materialクラスにさらなる変更を加える.
class Material
{
public FColor ambientFactor;
public FColor diffuseFactor;
public FColor specularFactor;
public float shininess;
public boolean usePerfectReflection;
public FColor catadioptricFactor; // 完全鏡面反射・屈折係数
public boolean useRefraction; // 屈折を使用するかどうか
public float refractionIndex; // 絶対屈折率
public Material()
{
ambientFactor = new FColor(0.01f, 0.01f, 0.01f);
diffuseFactor = new FColor(0.69f, 0.69f, 0.69f);
specularFactor = new FColor(0.30f, 0.30f, 0.30f);
shininess = 8;
usePerfectReflection = false;
catadioptricFactor = new FColor(0,0,0);
useRefraction = false; // デフォルトでは屈折を使用しない.
refractionIndex = 1.0; // 絶対屈折率はとりあえず1(真空と同じ)
}
}
useRefraction- 屈折を使用するかどうか
catadioptricFactor- 完全鏡面反射・屈折係数.前回から特に変更しないが屈折を使用する場合もこの係数を用いる.
refractionIndex- その物体の絶対屈折率
また,Sceneクラスにも以下の変更を施す.
class Scene
{
public ArrayList<Shape> shapes;
public ArrayList<LightSource> lightSources;
public FColor ambientIntensity;
public float globalRefractionIndex; // 大気の絶対屈折率
public Scene()
{
shapes = new ArrayList();
lightSources = new ArrayList();
ambientIntensity = new FColor(0.01f, 0.01f, 0.01f);
globalRefractionIndex = 1.000293; // 標準状態(1気圧20℃)における大気の屈折率
}
// ..以下略..
globalRefractionIndex- シーンが想定している大気(媒質)の絶対屈折率.デフォルトで1気圧20℃の空気の屈折率とする.
※ 厳密に言うと媒質の絶対屈折率も波長の関数であるため,絶対屈折率をRGB3チャンネルで定義すればプリズムなどによる分光の表現も可能になるが,複雑になる(だけでなく膨大な計算量となる)ためここでは単一の実数値として定義する.
rayTraceメソッドの変更
rayTraceメソッド(rayTraceRecursiveメソッド)を再帰呼び出しすることで光の屈折を実装する部分は,完全鏡面反射の場合と同じである.
レイの経路に関する注意事項
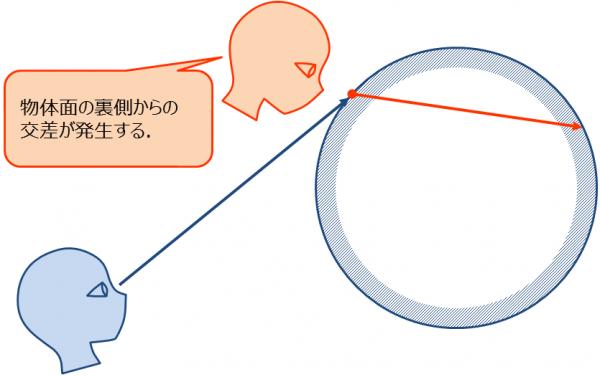
光の屈折の実装では,今までの実装の中で初めてレイが物体面の裏側から進入する場合がある(図8).
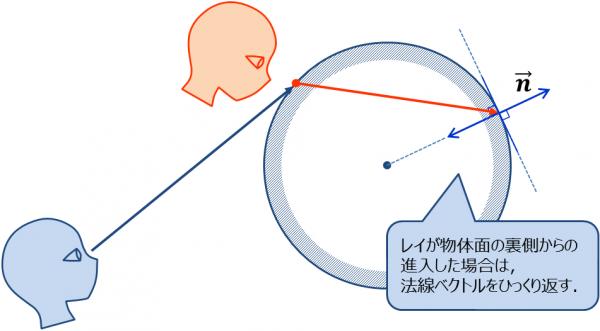
この場合,交点における法線ベクトルを反転する必要がある(図9).
視線ベクトルの進入方向を判定するには,視線ベクトルの逆ベクトル$$\vec{\bf v}$$と (反転を施す前の元の)法線ベクトル$$\vec{\bf n}$$との内積$$(\vec{\bf v}\cdot\vec{\bf n})$$をとり, その値の正負をチェックすれば良い. 値が正ならばレイは物体の表面からの進入しており,負ならば物体の裏面から進入している.
レイの進入方向によって,絶対屈折率$$\eta_{1},\eta_{2}$$の値の取り方も変わる. $$\eta_{1}$$は屈折前の媒質の絶対屈折率,$$\eta_{2}$$は屈折後の媒質の絶対屈折率である.
レイが物体の表面から進入した場合は,$$\eta_{1}$$=大気の絶対屈折率,$$\eta_{2}$$=物体の絶対屈折率となる.
レイが物体の裏面から進入した場合は,$$\eta_{1}$$=物体の絶対屈折率,$$\eta_{2}$$=大気の絶対屈折率となる.
(このことから分かるように,今回の実装では光線の経路は「大気→物体→大気」の順となることを前提としている. 物体から大気以外の物質に光線が出て行くことを想定していない.物体と視線との交点を見つけた場合に,それが大気との接点なのか他の物体との 接点なのかを判定するための処理はやや複雑になる.)
計算の効率化
屈折ベクトルおよび完全鏡面反射率の計算は,式を変形することで効率化できる.
p偏光反射率,s偏光反射率を以下のように変形する.
また屈折ベクトルの導出過程の式(6)から
$$\rho_{\perp}$$と$$\vec{\bf f}$$の一部に共通項ができた.
$$\displaystyle \eta_{r}=\frac{\eta_{2}}{\eta_{1}}$$,$$\Omega=\eta_{r}cos\theta_{2}-cos\theta_{1}$$と置いて,
入射ベクトル$$\vec{\bf i}$$はここでは視線ベクトル$$\vec{\bf d_{\cal e}}$$なので,それに対する屈折ベクトル$$\vec{\bf f_{\cal e}}$$は以下となる.
また$$cos\theta{1}$$,$$cos\theta{2}$$は以下となる.
$$\vec{\bf v}$$は視線ベクトルの逆ベクトルである.すなわち,$$\vec{\bf v}=-\vec{\bf d_{\cal e}}$$となる.
課題
課題3-3. 光の屈折を実装する
「課題3-2. 完全鏡面反射を実装する」のスケッチを改造して,光の屈折の処理を実装せよ.
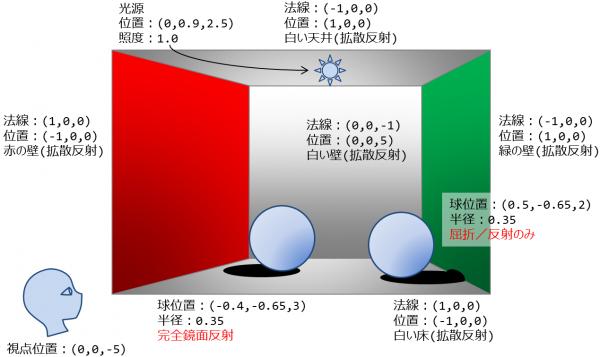
シーンの設定は以下のようにせよ(図10). 課題3-2とほぼ同じだが完全鏡面反射する球の位置と大きさが異なり,光を透過する球が追加されている.
- 物体は全部で7つ
- 球1(完全鏡面反射)
- 位置:$$(-0.4, -0.65, 3)$$,半径:$$0.35$$
- 質感は完全鏡面反射のみ
- 球2(屈折)
- 位置:$$(0.5, -0.65, 2)$$,半径:$$0.35$$
- 絶対屈折率$$1.51$$
- ソーダ石灰ガラス(普通のガラス)の絶対屈折率
- 質感は完全鏡面反射/屈折のみ
- 平面1(白い床)
- 法線:$$(0,1,0)$$,位置:$$(0,-1,0)$$, 拡散反射のみ
- 平面2(白い天井)
- 法線:$$(0,-1,0)$$,位置:$$(0,1,0)$$, 拡散反射のみ
- 平面3(右の緑の壁)
- 法線:$$(-1,0,0)$$,位置:$$(1,0,0)$$, 拡散反射のみ
- 平面4(左の赤の壁)
- 法線:$$(1,0,0)$$,位置:$$(-1,0,0)$$, 拡散反射のみ
- 平面5(白い奥壁)
- 法線:$$(0,0,-1)$$,位置:$$(0,0,5)$$, 拡散反射のみ
- 球1(完全鏡面反射)
- 光源は一つ
- 点光源
- 位置:$$(0,0.9,2.5)$$,照度:$$1.0$$
- 点光源
- シーン
- 大気の絶対屈折率は$$1.0$$
生成画像は以下のようになる.
球2のチェックポイントとしては,
- 球の輪郭側に近づくにつれて完全鏡面反射が強くなる
- 球全体としては後ろの風景の倒立像がみえる
という点に着目すること.
ヒント1
- 視線と交差する物体が屈折を使用する材質である場合
- 視線ベクトル$$\vec{\bf d_{\cal e}}$$を正規化する.
- $$\vec{\bf d’_{\cal e}}=\frac{1}{\left|\vec{\bf d_{\cal e}}\right|}\vec{\bf d_{\cal e}}$$
- (視線ベクトルは正規化されているとは限らない.)
- 視線ベクトルの逆ベクトル$$\vec{\bf v}$$を計算する.
- $$\vec{\bf v}=-\vec{\bf d’_{\cal e}}$$
- $$\vec{\bf v}$$と物体表面の法線ベクトル$$\vec{\bf n}$$の内積$$(\vec{\bf v}\cdot\vec{\bf n})$$を計算する.
- $$(\vec{\bf v}\cdot\vec{\bf n})\lt0$$の場合
- 屈折率$$\eta_{1}$$,$$\eta_{2}$$を入れ替える.
- 法線ベクトルを反転する.
- $$\vec{\bf n}\leftarrow-\vec{\bf n}$$
- 内積$$(\vec{\bf v}\cdot\vec{\bf n})$$を計算し直す.
- 一時変数$$\eta_{r}=\frac{\eta_{2}}{\eta_{1}}$$を計算する.
- $$cos\theta_{1}$$の値を計算する.
- $$cos\theta_{1}=(\vec{\bf v}\cdot\vec{\bf n})$$
- $$cos\theta_{2}$$の値を計算する.
- $$cos\theta_{2}=\frac{\eta_{1}}{\eta_{2}}\sqrt{\eta^{2}_{r}-\left(1-cos^{2}\theta_{1}\right)}$$
- 一時変数$$\Omega=\eta_{r}cos\theta_{2}-cos\theta_{1}$$を計算する.
- 正反射方向ベクトル$$\vec{\bf r_{\cal e}}$$を計算する.
- $$\vec{\bf r_{\cal e}}=2(\vec{\bf v}\cdot\vec{\bf n})\vec{\bf n}-\vec{\bf v}$$
- 屈折方向ベクトル$$\vec{\bf f_{\cal e}}$$を計算する.
- $$\vec{\bf f_{\cal e}}=\frac{\eta_{1}}{\eta_{2}}\vec{\bf d’_{\cal e}}-\frac{\eta_{1}}{\eta_{2}}\Omega\vec{\bf n}$$
- 正反射方向の半直線を作る.
- 始点:$$\vec{\bf p_{\cal i}}+\epsilon\vec{\bf r_{\cal e}}$$
- $$\vec{\bf p_{i}}$$:視線と物体の交点の位置ベクトル
- $$\epsilon$$:微小距離.ここでは$$\frac{1.0}{512}$$
- 方向:$$\vec{\bf r_{\cal e}}$$
- 始点:$$\vec{\bf p_{\cal i}}+\epsilon\vec{\bf r_{\cal e}}$$
- 屈折方向の半直線を作る.
- 始点:$$\vec{\bf p_{\cal i}}+\epsilon\vec{\bf f_{\cal e}}$$
- $$\vec{\bf p_{i}}$$:視線と物体の交点の位置ベクトル
- $$\epsilon$$:微小距離.ここでは$$\frac{1.0}{512}$$
- 方向:$$\vec{\bf f_{\cal e}}$$
- 始点:$$\vec{\bf p_{\cal i}}+\epsilon\vec{\bf f_{\cal e}}$$
- 完全鏡面反射率$$c_{r}$$および透過率$$c_{t}$$を計算する.
- p偏光反射率$$\rho_{\parallel}$$を計算する.
- $$\rho_{\parallel} = \frac{\eta_{r}cos\theta_{1}-cos\theta_{2}}{\eta_{r}cos\theta_{1}+cos\theta_{2}}$$
- s偏光反射率$$\rho_{\perp}$$を計算する.
- $$\rho_{\perp} = \frac{-\Omega}{\eta_{r}cos\theta_{2}+cos\theta_{1}} $$
- 鏡面反射率$$c_{r}$$を計算する.
- $$c_{r}=\frac{1}{2}\left(\rho^{2}_{\parallel}+\rho^{2}_{\perp}\right)$$
- 透過率$$c_{r}$$を計算する.
- $$c_{t}=1-c_{r}$$
- p偏光反射率$$\rho_{\parallel}$$を計算する.
- 完全鏡面反射光の放射輝度を計算する.
- 正反射方向に光線追跡を行う.
- 放射輝度に$$k_{f}c_{r}R_{re}$$を足し合わせる.
- 屈折光の放射輝度を計算する.
- 屈折方向に光線追跡を行う.
- 放射輝度に$$k_{f}c_{t}R_{fe}$$を足し合わせる.
- 視線ベクトル$$\vec{\bf d_{\cal e}}$$を正規化する.



0 Comments.