The Textbook of RayTracing @TDU

参考文献: 千葉 則茂，村岡 一信(著)「CによるCGレイトレーシング」(サイエンス社)

完全鏡面反射

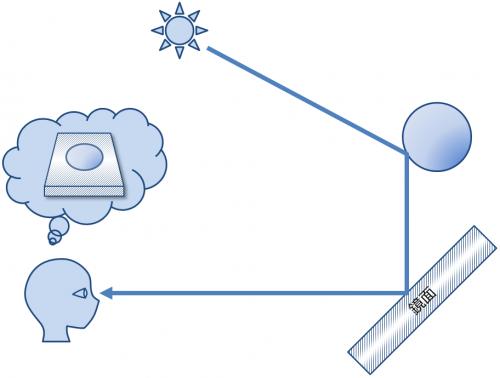
鏡やクロム球の表面などで，入射した光がほぼ完全に反射する現象を完全鏡面反射という(図1)．

完全鏡面反射する面では，他の物体の表面で反射した光が見えていると言える(図2)．

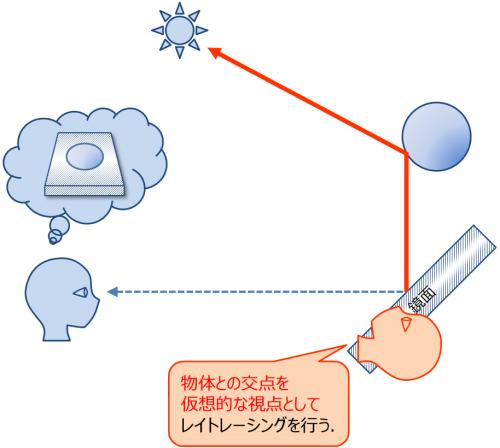
これをレイトレーシング法で再現することは容易である．完全鏡面反射する表面を再現するには，物体表面の色を決める処理の中で視線と物体の交点を， 仮想的な視点としてレイトレーシングを行えばよい(図3)．

この仮想的な視点の位置と視線方向は以下のようになる．

• 仮想的な視点の位置
  • 物体と(大元の)視線との交点$$\vec{\bf p_{\cal i}}$$
• 仮想的な視点の視線方向
  • (大元の)視線方向の，交点$$\vec{\bf p_{\cal i}}$$における正反射ベクトル$$\vec{\bf r_{\cal e}}=2\left(\vec{\bf v}\cdot\vec{\bf n}\right)\vec{\bf n}-\vec{\bf v}$$
    • $$\vec{\bf n}$$：交点$$\vec{\bf p_{\cal i}}$$における法線ベクトル
    • $$\vec{\bf v}$$：(大元の)視線ベクトルの逆ベクトル

物体表面の輝度$$L_{r}$$を以下のように変更する．

• $$R_{a}$$：環境光の反射光の放射輝度
• $$R_{di}$$：i番目の光源からの直接光の拡散反射光の放射輝度
• $$R_{si}$$：i番目の光源からの直接光の鏡面反射光の放射輝度
• $$R_m$$：完全鏡面反射光の放射輝度

また，完全鏡面反射光の輝度$$R_m$$は以下である．

• $$k_{f}$$：完全鏡面反射係数
• $$R_{re}$$：(前述の)$$\vec{\bf r_{\cal e}}$$方向で得られる輝度

完全鏡面反射の実装

仮想的な視点の位置と方向

「シャドウレイ」の件と同様に始点位置に注意する．
（大元の）視線ベクトルと物体の交点をそのままレイの始点として使用するとうまくいかない(説明省略)．

Materialクラスの変更

前節の完全鏡面反射に対応するため，Materialクラスに変更を加える．

class Material 
{
  public FColor ambientFactor;
  public FColor diffuseFactor;
  public FColor specularFactor;
  public float shininess;
  
  public boolean usePerfectReflectance; // 完全鏡面反射を使うかどうか
  public FColor catadioptricFactor;     // 完全鏡面反射係数
  
  public Material()
  {
    ambientFactor  = new FColor(0.01f, 0.01f, 0.01f);
    diffuseFactor  = new FColor(0.69f, 0.69f, 0.69f);
    specularFactor = new FColor(0.30f, 0.30f, 0.30f);
    shininess = 8;    
    
    usePerfectReflectance = false;          // デフォルトでは完全鏡面反射を使わない
    catadioptricFactor = new FColor(0,0,0); // 反射係数もゼロ
  }  
}

usePerfectReflectance(boolean)

完全鏡面反射を使うかどうか

catadioptricFactor(FColor)

完全鏡面反射係数

完全鏡面反射の反射光の計算は時間的コストがかかるため，完全鏡面反射を使用しない場合はその計算を行わないようにする． userPerfectReflectanceはboolean型の属性であり，trueである場合にのみ完全鏡面反射光の計算を行う．

catadioptricFactorはFColor型の属性であり，前述の式の中の$$k_{f}$$に相当する．

rayTraceメソッドの変更

完全鏡面反射を実装するにはrayTraceメソッドの中でrayTraceメソッドを呼び出す，つまり再帰呼び出しを使って実装することになる(リスト1)．

FColor rayTrace(Scene scene, Ray ray)
{
    // ..中略.. 
    Ray reRay; // 視線の正反射方向の半直線
    rayTrace(scene, reRay);
    // ..中略.. 
}

再帰呼び出しを用いる際は，再帰呼び出しの終了条件に注意する必要がある． 迂闊に何の制限もなくリスト1のような実装を用いると条件によってはrayTraceメソッドが無限に再帰呼び出しされる可能性がある．

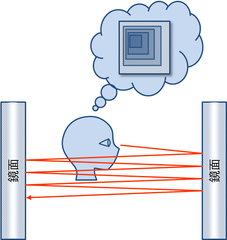
再帰しているときに完全鏡面反射しない物体に交差するか，別の物体と交差しなければ自然に再帰呼び出しは止まるが， 完全鏡面反射する物体が向かい合わせになっているような場合は再帰呼び出しが止まらなくなる(図4)．

これを防ぐため再帰呼び出しの回数には決め打ちの制限を設ける． rayTraceメソッドは以下のような構造となる(リスト2)．

// 最大の再帰呼び出し回数
final int MAX_RECURSION = 8;

// 新たに再帰呼び出し用のメソッドを用意する
FColor rayTraceRecursive(Scene scene, Ray ray, int recusionLevel)
{
   if ( recursionLevel > MAX_RECURSION ) // 再帰呼び出しの回数が制限を超えている場合 
   {
      // 交差なしとして扱う
      return null;
   }
   else // 再帰呼び出しの回数が制限以内の場合
   {
      // 放射輝度の計算
      // ..中略..

      if (/* 完全鏡面反射を使う場合*/)
      {
        // 現在の再帰呼び出し回数(recursionLevel)を増やして呼び出す．
        Ray reRay; // 視線の正反射方向の半直線
        rayTraceRecursive(scene, reRay, recursionLevel + 1);
      }

     // ..中略..
  }
}

// いままでの rayTraceメソッドは rayTraceRecursiveメソッドを呼び出すだけ
FColor rayTrace(Scene scene, Ray ray)
{
    return rayTraceRecursive(scene, eye_ray, 0);
}

新たにrayTraceRecursiveメソッドを追加し，今までのrayTraceメソッドはこの新しいメソッドを単に呼び出すだけとなった．

rayTraceRecursiveメソッドは，一つを除いてrayTraceメソッドと同じ引数を持つ．rayTraceRecursiveメソッドの 最後の引数recursionLevelは現在の再帰呼び出しの回数を表している．rayTraceメソッドではこの引数をゼロとして rayTraceRecursiveメソッドを呼び出している．21行目のようにrayTraceRecursiveメソッドの中で再帰呼び出しを行う場合は このrecursionLevelに1を足して再帰呼び出しを行う．

再帰呼び出しが重なるたびにrecursionLevelの値が増加していくが，この値が最大数である決め打ちの MAX_RECURSIONを超えている場合は何もせずに終了する．こうすることで再帰呼び出しが停止しなくなることを防ぐ．

recursionLevelがMAX_RECURSION未満の場合は，いままでのrayTraceメソッド相当の処理を行う．

課題

課題3-2. 完全鏡面反射を実装する

「課題3-1. 付影処理を実装する」のスケッチを改造して完全鏡面反射の処理を実装せよ．

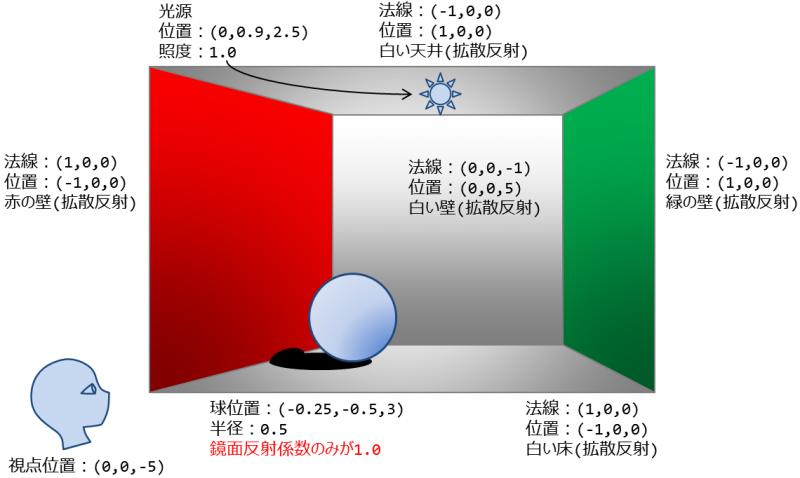
シーンの設定は以下のようにせよ(図5)．

• 物体は全部で6つ
  1. 球
     • 位置：$$(-0.25, -0.5, 3)$$，半径：$$0.5$$
     • 質感は完全鏡面反射のみ
  2. 平面1(白い床)
     • 法線：$$(0,1,0)$$，位置：$$(0,-1,0)$$, 拡散反射のみ
  3. 平面2(白い天井)
     • 法線：$$(0,-1,0)$$，位置：$$(0,1,0)$$, 拡散反射のみ
  4. 平面3(右の緑の壁)
     • 法線：$$(-1,0,0)$$，位置：$$(1,0,0)$$, 拡散反射のみ
  5. 平面4(左の赤の壁)
     • 法線：$$(1,0,0)$$，位置：$$(-1,0,0)$$, 拡散反射のみ
  6. 平面5(白い奥壁)
     • 法線：$$(0,0,-1)$$，位置：$$(0,0,5)$$, 拡散反射のみ
• 光源は一つ
  1. 点光源
     • 位置：$$(0,0.9,2.5)$$，光の強さ：$$(1.00, 1.00, 1.00)$$

生成画像は以下のようになる．

図6. 生成画像

ヒント１

ヒント２