第４回

Leave a comment (0) Go to comments

[—ATOC—] 1 [—AUTO_SECTION_NUMBER—]

追加課題 [—EXCLUDE—]

第4回はレポート作成などの作業時間です．以下は進みが早い人用の課題です．指示がない限りとりくむ必要はありません．

課題EX-1. 規則的に球を表示させる

前提：少なくとも課題2-3. raytrace関数を実装するを実装していること．

以下のようなシーンを作成せよ．

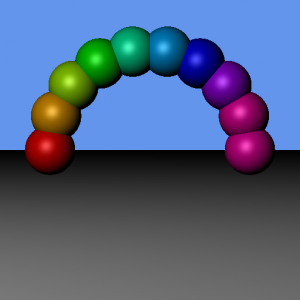
scene_ex1_10
図1. 生成画像(球の数=10の場合)

scene_ex1_20
図2. 生成画像(球の数=20の場合)

scene_ex1_50
図3. 生成画像(球の数=50の場合)

  • 球の数
    • 後から変更可能にすること(マクロ定数を用意しておく)
  • 球の位置
    • 座標(0,0,10)を中心として半径2.0の半円の円周上に等間隔に配置する
  • 球の半径
    • 0.5
  • 球の色
    • HSV表色系で左から赤→緑→青→紫(色相が0°→360°へ変化する)と連続的に変化すること．
    • 拡散反射光で色を表現すること．

以下はHSV表色系の色をRGB表色系に変換する関数である．

void hsv_to_rgb(colorf_t *out_col, float h, float s, float v)
{
  float H = 360 * h;
  float S = s;
  float V = v;
  int Hi = floor(H/60);
  float f = H/60 - Hi;
  float p = V*(1-S);
  float q = V*(1-f*S);
  float t = V*(1-(1-f)*S);

  if ( Hi == 0 )
    SET_COLOR((*out_col), V, t, p)
  else if ( Hi == 1)
    SET_COLOR((*out_col), q, V, p)
  else if ( Hi == 2)
    SET_COLOR((*out_col), p, V, t)
  else if ( Hi == 3)
    SET_COLOR((*out_col), p, q, V)
  else if ( Hi == 4)
    SET_COLOR((*out_col), t, p, V)
  else if ( Hi == 5)
    SET_COLOR((*out_col), V, p, q)
}
  • 引数
    1. out_col
      • 【出力】RGB値を入れるためのcolorf_t構造体のポインタ
    2. h
      • 【入力】色相(hue)．[0,1]の実数値(0°から360°に対応する)
    3. s
      • 【入力】彩度(satuation)．[0,1]の実数値
    4. v
      • 【入力】明度(value)．[0,1]の実数値
  • 戻り値
    • なし

ヒント

+ クリックで表示 クリックで非表示

x座標にcos関数，y座標にsin関数を用いる．

C言語ではM_PIという円周率の値の入ったマクロを用いることが多いが，厳密なC89規格には存在しない．
そのため円周率が必要ならば，ソースコードのどこかで以下のようなマクロを定義しておけばよいだろう．

#define M_PI 3.141592653589f
-クリックで非表示

課題EX-2. 視点を変える

前提：少なくとも課題2-3. raytrace関数を実装するを実装していること．

任意の始点から任意の注視点を観察できるように変更する．
scene_t構造体を以下のように変更し，視点を変えられるようにせよ．

typedef struct
{
  vector_t eye_position;        /* 【追加】視点位置 */
  vector_t look_at;             /* 【追加】注視点 */
  float screen_distance;        /* 【追加】スクリーンまでの距離 */

  shape_t *shapes;              /* 物体リストへのポインタ */
  size_t num_shapes_capacity;   /* 物体リストの最大格納数 */
  size_t num_shapes;            /* 物体リストに実際に格納されている数 */
  light_t *lights;              /* 光源リストへのポインタ */
  size_t num_lights_capacity;   /* 光源リストの最大格納数 */
  size_t num_lights;            /* 光源リストに実際に格納されている数 */
  colorf_t ambient_illuminance; /* 環境光の強さ(RGB) */
} scene_t;

視点位置$$\vec{\bf p_{e}}$$，注視点$$\overrightarrow{\bf p_{lookat}}$$，スクリーンまでの距離$$m$$の関係は図4のようになっている．

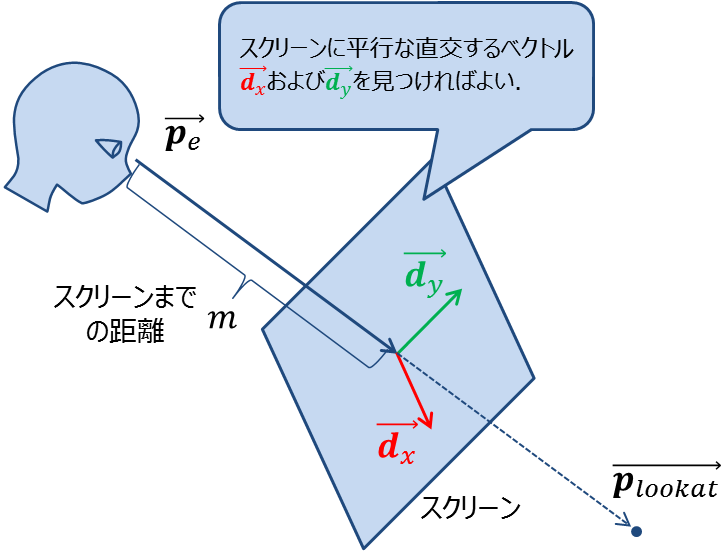
lookat
図4. 任意の位置のスクリーン

図5は課題EX-1. 規則的に球を表示させるで視点を変えて レイトレーシングを行った例である(わかりやすいように影を付けてあるが必須ではない)．

scene_ex2
図5. 視点を変えてレイトレーシングした例

ヒント１

+ クリックで表示 クリックで非表示

ベクトルの外積の性質を利用する。

計算結果がスカラーとなるベクトルの内積と異なり，ベクトルの外積はベクトルとなる．
その方向は，二つのベクトルが張る平面(二つのベクトルを含む平面)に垂直なベクトルとなる．

ベクトル$$\vec{\bf a}, \vec{\bf b}$$の外積$$\left(\vec{\bf a}\times\vec{\bf b}\right)$$は，ベクトル$$\vec{\bf b}$$を ベクトル$$\vec{\bf a}$$に近づけるときの右ねじの向きのベクトルとなる(左手系の場合)．

$$\left(\vec{\bf a}\times\vec{\bf b}\right)$$は，ベクトル$$\vec{\bf a}, \vec{\bf b}$$と直交するベクトルとなる．

この問題ではベクトルの外積計算を2回使う．かつ，決め打ちの上方向ベクトル$$\vec{\bf up}=(0,1,0)$$が必要となる．

-クリックで非表示

ヒント２

+ クリックで表示 クリックで非表示
\(\begin{array} \\ \vec{\bf up}=(0,1,0) \\ \overrightarrow{\bf d_{lookat}}=normalize\left(\overrightarrow{\bf p_{lookat}}-\vec{\bf p_{e}}\right) \\ \vec{\bf d_{x}}=normalize\left(\vec{\bf up}\times\overrightarrow{\bf d_{lookat}}\right) \\ \vec{\bf d_{y}}=normalize\left(\overrightarrow{\bf d_{lookat}}\times\vec{\bf d_{x}}\right) \\ \vec{\bf p_{w}}=\vec{\bf p_{e}}+m\overrightarrow{\bf d_{lookat}}+f_{x}\vec{\bf d_{x}} + f_{y}\vec{\bf d_{y}} \\ \vec{\bf d_{e}}=\vec{\bf p_{w}}-\vec{\bf p_{e}} \\ f_{x} = \frac{2x_{s}}{(W-1) -1} \\ f_{y} = \frac{-2y_{s}}{(H-1) +1} \\ \end{array}\)


  • $$\vec{\bf d_{e}}$$
    • 視線ベクトル
  • $$\vec{\bf p_{w}}$$
    • スクリーン上のピクセル位置(三次元座標)
  • $$x_{s},y_{s}$$
    • スクリーン座標(二次元座標)
-クリックで非表示

課題EX-3. 画面サイズを変える

前提：課題EX-2. 視点を変えるを実装していること．

出力画像サイズは今まで固定で512×512であった．これを任意の解像度に対応できるようにする．
scene_t構造体に以下の変更を加える．

typedef struct
{
  size_t width;                 /* 【追加】出力画像の幅 */
  size_t height;                /* 【追加】出力画像の高さ */

  vector_t eye_position;        /* 視点位置 */
  vector_t look_at;             /* 注視点 */
  float screen_distance;        /* スクリーンまでの距離 */

  shape_t *shapes;              /* 物体リストへのポインタ */
  size_t num_shapes_capacity;   /* 物体リストの最大格納数 */
  size_t num_shapes;            /* 物体リストに実際に格納されている数 */
  light_t *lights;              /* 光源リストへのポインタ */
  size_t num_lights_capacity;   /* 光源リストの最大格納数 */
  size_t num_lights;            /* 光源リストに実際に格納されている数 */
  colorf_t ambient_illuminance; /* 環境光の強さ(RGB) */
} scene_t;

図6は実行例である．

scene_ex3
図6. 実行例

縦長，横長，正方形のすべての場合に対応すること．

ヒント１

+ クリックで表示 クリックで非表示

方法はいろいろあるが，ここでは指定された幅と高さのうち大きい方が三次元空間中の2.0の長さになるようにする．

-クリックで非表示

ヒント２

+ クリックで表示 クリックで非表示

指定された出力画像のサイズをチェックして，対応するスクリーン上の大きさを変数として保持する．
画像の幅を$$W$$，画像の高さを$$H$$，スクリーンの幅を$$W_{s}$$，スクリーンの高さを$$H_{s}$$とすると．

\(\displaystyle \begin{array} \\ W_{s}=\left\{\begin{array} \\ 2 && (W \ge H) \\ \frac{2W}{H} && (W \lt H)\\ \end{array} \right. \\ H_{s}=\left\{\begin{array} \\ 2 && (W \le H) \\ \frac{2H}{W} && (W \gt H)\\ \end{array} \right. \\ \end{array}\)


$$f_{x}$$, $$f_{y}$$は以下のように変更される．

\(\displaystyle \begin{array} \\ f_{x} = \frac{W_{s}x_{s}}{W-1}-\frac{W_{s}}{2} \\ f_{x} = \frac{-H_{s}y_{s}}{H-1}+\frac{H_{s}}{2} \\ \end{array}\)


-クリックで非表示

余力のある方向け

スクリーンまでの距離を小さくとると画角が広くなる．
逆に画角からスクリーン距離を決めるような実装はできるだろうか．

※ カメラ(視線)のパラメータとして，視点位置，注視点，画角の三つを指定させるシステムは一般的である．

ヒント：tan

課題EX-4. 円錐を表示させる

前提：少なくとも課題2-3. raytrace関数を実装するを実装していること．

形状として円錐を実装する．

中心位置$$\vec{\bf p_{\cal c}}=(c_{x}, c_{y}, c_{z})$$，高さ$$h$$,半径$$r$$の円錐の方程式は以下である(ベクトル方程式ではない)(図7)．

\( (x-c_{x})^{2}+(z-c_{z})^2=\left(\frac{r}{h}\right)^{2}(y-h-c_{y})^{2} \ldots (1) \)


図7. 円錐

上記の方程式と半直線$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d}$$の解析表示，

\(\left\{\begin{array} \\ x = s_{x} + t d_{x} \\ y = s_{y} + t d_{y} \\ z = s_{z} + t d_{z} \\ \end{array}\right.\)


を連立してtに関する二次方程式に整理し，tについて解けばよい．
ただし，これによって求まった交点と，位置$$\vec{\bf p_{\cal c}}$$とのy軸距離が$$[-h,0]$$の範囲内である場合のみ交点を持つ．．

交点$$\vec{\bf p_{\cal i}}=(i_{x},i_{y},i_{z})$$における法線ベクトル$$\vec{\bf n}=(n_{x},n_{y},n_{z})$$を求めるには， 式(1)を陰関数表示にして，$$x,y,z$$の各次元で偏微分すればよい(接平面の法線ベクトルが求まる．この方法は曲面一般に使用できる．)．

\(\displaystyle \begin{array} \\ F(x,y,z)=(x-c_{x})^{2}+(z-c_{z})^2-\left(\frac{r}{h}\right)^{2}(y-h-c_{y})^{2} \\ n_{x}=\left.\frac{\partial F(x,y,z)}{\partial x}\right|_{(x,y,z)=(i_{x},i_{y},i_{z})} = 2(i_{x}-c_{x}) \\ n_{y}=\left.\frac{\partial F(x,y,z)}{\partial y}\right|_{(x,y,z)=(i_{x},i_{y},i_{z})} = -2\left(\frac{r}{h}\right)^{2}(i_{y}-c_{y}-h) \\ n_{z}=\left.\frac{\partial F(x,y,z)}{\partial z}\right|_{(x,y,z)=(i_{x},i_{y},i_{z})} = 2(i_{z}-c_{z})\\ \end{array}\)


円柱の見た目はおおよそ図8のようになる．図8は，位置$$\vec{\bf p_{\cal c}}=(0,-1,5)$$にある半径1.0，高さ2.0の円錐である．

scene_ex4
図8. 生成画像

ヒント

+ クリックで表示 クリックで非表示

以下のような構造体を新たに作る．

typedef struct
{
    vector_t position; /* 位置 */
    float radius;      /* 半径 */
    float height;      /* 高さ */
} cone_t;

shape_t構造体を変更する．

typedef enum
  {
    ST_SPHERE, /* 球 */
    ST_PLANE,  /* 平面 */
    ST_CONE,   /* 【追加】円錐 */
  } shape_type;
typedef struct
{
  shape_type type;     /* 球 or 平面 */
  union
  {
    sphere_t sphere;   /* 球の情報 */
    plane_t plane;     /* 平面の情報 */
    cone_t cone;       /* 【追加】円錐 */
  } data;

  material_t material; /* 物体表面の質感 */
} shape_t;

intersection_test関数を変更することで実装することができる．

-クリックで非表示

余力のある方向け

この方法で表示させた円錐には底面がない．底面を表示するにはどうしたらいいだろうか．

ヒント：平面との交差判定を併用する

課題EX-5. 円柱を表示させる

前提：少なくとも課題2-3. raytrace関数を実装するを実装していること．

形状として円柱を実装する．

中心位置$$\vec{\bf p_{\cal c}}=(c_{x}, c_{y}, c_{z})$$，高さ$$h$$，半径$$r$$の円柱の方程式は以下である(ベクトル方程式ではない)(図9)．

\( (x-c_{x})^{2}+(z-c_{z})^2=r^{2} \ldots (1) \)

※ この式は実際は高さ無限の円柱であるため，$$h$$の値は式には出てこない．


図9. 円柱

上記の方程式と半直線$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d}$$の解析表示，

\(\left\{\begin{array} \\ x = s_{x} + t d_{x} \\ y = s_{y} + t d_{y} \\ z = s_{z} + t d_{z} \\ \end{array}\right.\)


を連立してtに関する二次方程式に整理し，tについて解けばよい．
ただし，これによって求まった交点と，位置$$\vec{\bf p_{\cal c}}$$とのy軸距離が$$\left[-\frac{h}{2},\frac{h}{2}\right]$$の範囲内である場合のみ交点を持つ．．

交点$$\vec{\bf p_{\cal i}}=(i_{x},i_{y},i_{z})$$における法線ベクトル$$\vec{\bf n}=(n_{x},n_{y},n_{z})$$を求めるには， 式(1)を陰関数表示にして，$$x,y,z$$の各次元で偏微分すればよい(接平面の法線ベクトルが求まる．この方法は曲面一般に使用できる．)．

\(\displaystyle \begin{array} \\ F(x,y,z)=(x-c_{x})^{2}+(z-c_{z})^{2}-r^{2} \\ n_{x}=\left.\frac{\partial F(x,y,z)}{\partial x}\right|_{(x,y,z)=(i_{x},i_{y},i_{z})} = 2(i_{x}-c_{x}) \\ n_{y}=\left.\frac{\partial F(x,y,z)}{\partial y}\right|_{(x,y,z)=(i_{x},i_{y},i_{z})} = 0 \\ n_{z}=\left.\frac{\partial F(x,y,z)}{\partial z}\right|_{(x,y,z)=(i_{x},i_{y},i_{z})} = 2(i_{z}-c_{z})\\ \end{array}\)


円柱の見た目はおおよそ図10のようになる．図10は，位置$$\vec{\bf p_{\cal c}}=(0,0,5)$$にある半径1.0，高さ1.0の円錐である．

scene_ex5
図10. 生成画像

ヒント

+ クリックで表示 クリックで非表示

以下のような構造体を新たに作る．

typedef struct
{
    vector_t position; /* 位置 */
    float radius;      /* 半径 */
    float height;      /* 高さ */
}  cylinder_t;

shape_t構造体を変更する．

typedef enum
  {
    ST_SPHERE,   /* 球 */
    ST_PLANE,    /* 平面 */
    ST_CYLINDER, /* 【追加】円柱 */
  } shape_type;
typedef struct
{
  shape_type type;     /* 球 or 平面 */
  union
  {
    sphere_t sphere;     /* 球の情報 */
    plane_t plane;       /* 平面の情報 */
    cylinder_t cylinder; /* 【追加】円柱 */
  } data;

  material_t material; /* 物体表面の質感 */
} shape_t;

intersection_test関数を変更することで実装することができる．

-クリックで非表示

余力のある方向け

この方法で表示させた円柱には天井と底面がない．天井と底面を表示するにはどうしたらいいだろうか．

ヒント：平面との交差判定を併用する

課題EX-6. フォグ

前提：少なくとも課題2-3. raytrace関数を実装するを実装していること．

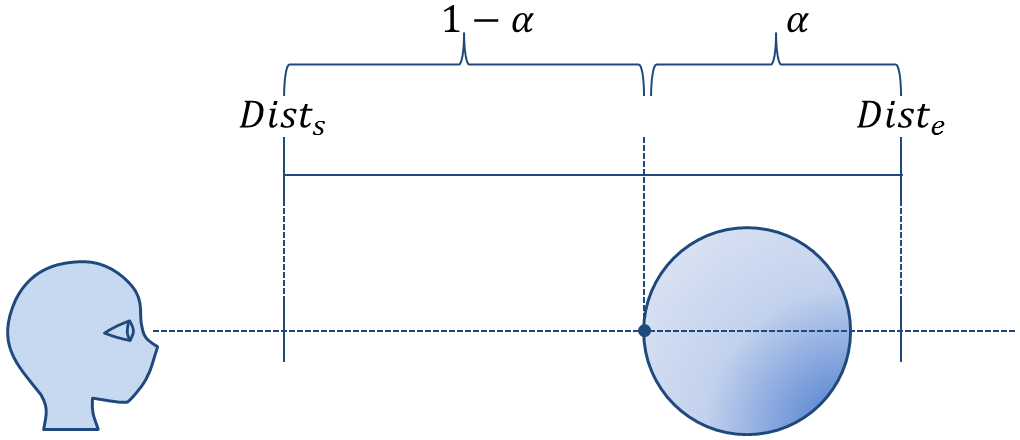
フォグとは空気遠近法ともいい，遠くの物体ほど背景色に近くなる表現である．以下のような生成画像となる．

scene_ex6
図11. フォグの表現

パラメータは以下である．

  • $$Dist_{s}$$
    • フォグをつける最小の距離
  • $$Dist_{e}$$
    • フォグをつける最大の距離

ヒント1

+ クリックで表示 クリックで非表示

scene_t構造体に以下のような変更が必要である．

typedef struct
{
  shape_t *shapes;              /* 物体リストへのポインタ */
  size_t num_shapes_capacity;   /* 物体リストの最大格納数 */
  size_t num_shapes;            /* 物体リストに実際に格納されている数 */
  light_t *lights;              /* 光源リストへのポインタ */
  size_t num_lights_capacity;   /* 光源リストの最大格納数 */
  size_t num_lights;            /* 光源リストに実際に格納されている数 */
  colorf_t ambient_illuminance; /* 環境光の強さ(RGB) */

  int use_fog;                  /* 【追加】フォグを使うかどうか */
  float fog_start_dist;         /* 【追加】フォグをつける最小の距離 */
  float fog_end_dist;           /* 【追加】フォグをつける最大の距離 */
} scene_t;
-クリックで非表示

ヒント2

+ クリックで表示 クリックで非表示

距離の値にしたがって背景色と物体の色を線形補間する．

lerp

-クリックで非表示

課題EX-7. トゥーンシェーディング

前提：少なくとも課題2-3. raytrace関数を実装するを実装していること．

トゥーンシェーディングとは，陰影を意図的に不連続にしたセルアニメのようなシェーディングである． 図12のようなシェーディングが可能になるように，raytrace関数を変更せよ．

scene_ex7
図12. 生成画像

パラメータは以下である．

  • $$N_{t}$$
    • 明度の段階．0ならばトゥーンシェーディングを使用しない．
  • $$C^{RGB}_{E}$$
    • 輪郭線の色
  • $$E_{t}$$
    • 輪郭線の強さ.[0,1]の範囲で，0が最も細く(非表示)，1が最も太い．

ヒント1

+ クリックで表示 クリックで非表示

この課題は二つの機能の合成である．

  • 陰影を離散化すること．
    • 拡散反射光の輝度も鏡面反射光の輝度も面の法線ベクトルと，光の入射ベクトルのなす角に依存して変化することを利用する．
  • エッジをつけること．
    • 面の法線ベクトルと視線ベクトル(あるいはその逆ベクトル)とのなす角に着目する．

toon
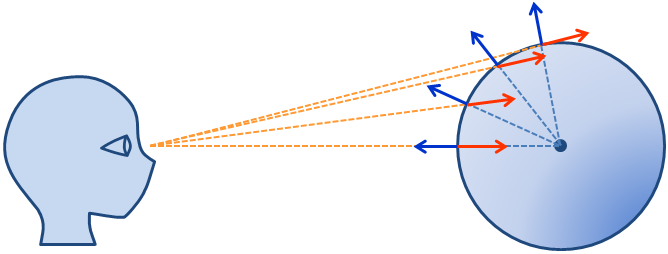
図13. 法線ベクトルと視線ベクトル

なお，material_tに以下のような変更が必要である．

typedef struct
{
  colorf_t ambient_ref;   /* 環境光反射率(RGB) */
  colorf_t diffuse_ref;   /* 拡散反射率(RGB) */
  colorf_t specular_ref;  /* 鏡面反射率(RGB) */
  float shininess;        /* 光沢度 */
  
  size_t toon_shading;    /* 【追加】明度の段階(0ならトゥーンシェーディングを使用しない) */
  colorf_t edge_color;    /* 【追加】輪郭線の色 */
  float edge_thickness;   /* 【追加】輪郭の太さ */
} material_t;
-クリックで非表示

ヒント2

+ クリックで表示 クリックで非表示
  • 連続的な勾配から不連続な勾配を作るにはfloor関数やceil関数を用いる．
    • floor関数もceil関数も与えられた実数に近い整数を返す．
    • しかし，内積＝ベクトルのなす角の余弦である．値の範囲は…
  • ベクトルの内積は，なす角の余弦であることに注意する．その勾配は線形ではない．
    • 一度，勾配を線形に直す必要がある．
  • エッジを表示するのは，法線ベクトルと視線ベクトル(あるいはその逆ベクトル)のなす角が$$E_{t}$$以上だったら，という条件が使える．
    • 条件に合致したら他の陰影の計算をせずに，輪郭線の色$$C^{RGB}_{E}$$を使う．
-クリックで非表示

ヒント3

+ クリックで表示 クリックで非表示

拡散反射光や鏡面反射光の計算に使う内積の値を$$A$$とする．トゥーンシェーディングを実現するために加工した$$A$$の値を$$A’$$とすると，以下のようになる．

\( A’=\frac{1}{N_{t}}\lceil N_{t}(1-\frac{2}{\pi}acos(A))\rceil \)

$$A$$の値はなす角の余弦である，従って以下のような勾配を持っている．

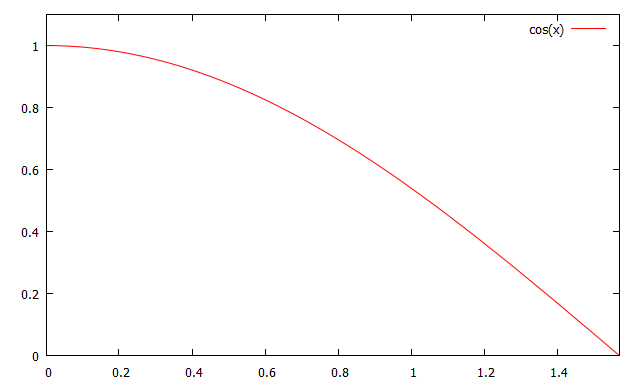
toon_curve_01

たとえば，これを10段階に離散化したい場合$$A’=\frac{1}{10}\lceil10A\rceil$$といった変換が考えられる．

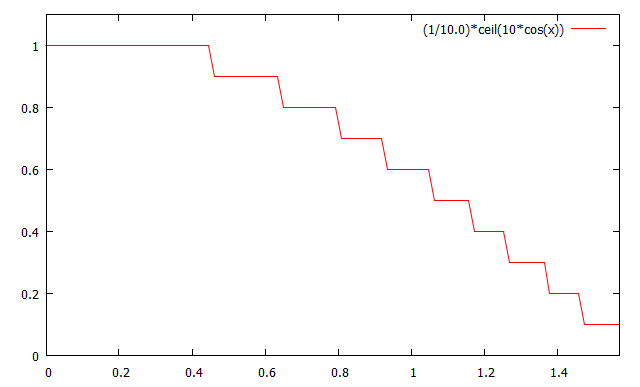
toon_curve_02

しかし，この変換だと各段階の長さが一定していない．そこで，余弦関数の逆関数(アークコサイン)を使って勾配を線形に変換する．

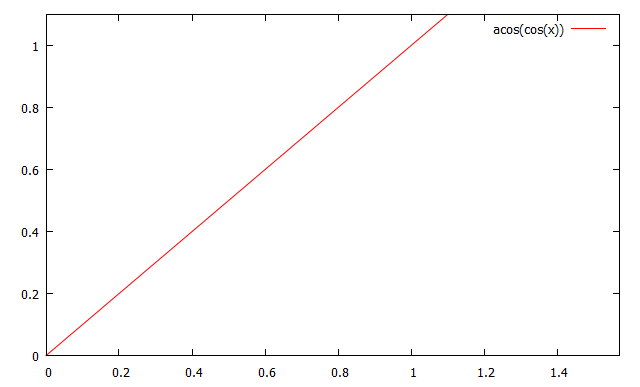
toon_curve_03

アークコサインの値域は$$[0,\pi]$$だが，Aの値は$$[0,1]$$の範囲なので，結局$$\left[0,\frac{\pi}{2}\right]$$である． アークコサインの値を$$\frac{\pi}{2}$$で割って，値域を$$[0,1]$$に押し込める．

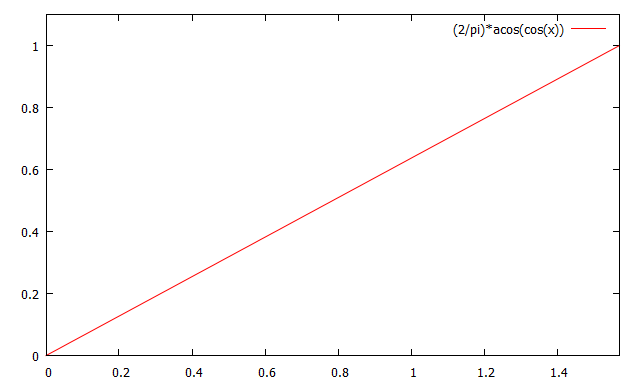
toon_curve_04

勾配が右肩上がりで，もとの余弦の勾配と逆なので反転する．

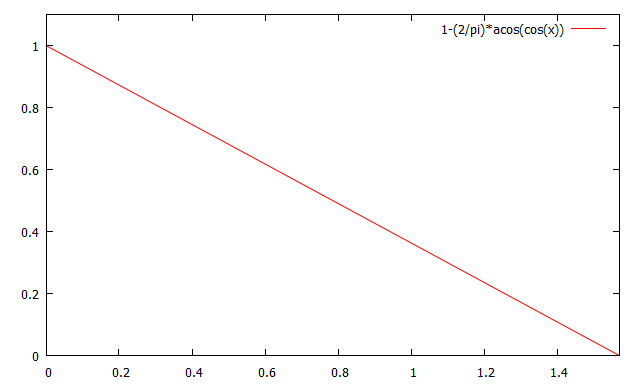
toon_curve_05

あとはこの値をceil関数を使って離散化すれば良い．つまり$$\frac{1}{10}\lceil 10(1-\frac{2}{\pi}acos(A))\rceil$$となる．

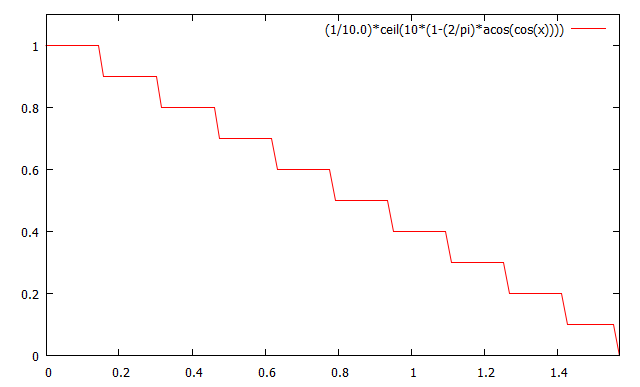
toon_curve_06

-クリックで非表示

Leave a Comment


NOTE - You can use these HTML tags and attributes:
<a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>