発展課題
第4回はレポート作成などの作業時間です.以下は進みが早い人用の課題です.指示がない限りとりくむ必要はありません.
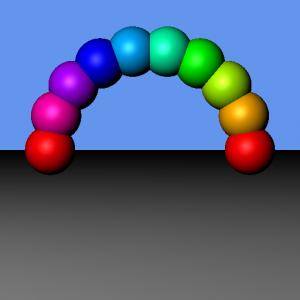
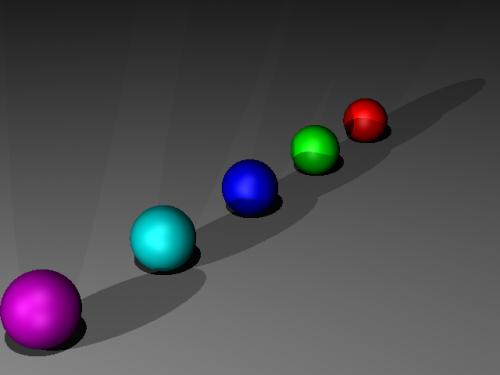
課題EX-1. 規則的に球を表示させる
前提:少なくとも「課題2-6 物体ごとに色を変更する」を実装していること.
以下のようなシーンを作成せよ.
- 球の数
- 変更可能にすること(定数を用意しておく).
- 球の位置
- 座標(0,0,10)を中心として半径2.0の半円の円周上に等間隔に配置する
- 球の半径
- 0.5
- 球の色
- HSV表色系で右から赤→緑→青→紫→赤(色相が0°→360°へ変化する)と連続的に変化すること.
- 拡散反射光で色を表現すること.
以下はHSV表色系の色をRGB表色系に変換するメソッドである.
FColor hsvToRgb(float hue, float sat, float val)
{
float H = constrain(hue, 0, 359);
float S = constrain(sat, 0, 1);
float V = constrain(val, 0, 1);
int Hi = (int)floor(H/60);
float f = H/60 - Hi;
float p = V * (1 - S);
float q = V * (1 - f*S);
float t = V * (1 - (1-f)*S);
FColor res = new FColor();
switch(Hi)
{
case 0 : res.set(V, t, p); break;
case 1 : res.set(q, V, p); break;
case 2 : res.set(p, V, t); break;
case 3 : res.set(p, q, V); break;
case 4 : res.set(t, p, V); break;
case 5 : res.set(V, p, q); break;
}//switch
return res;
}
引数
hue- 色相(hue).$$[0,359]$$の実数値.
sat- 彩度(satuation).$$[0,1]$$の実数値.
val- 明度(value).$$[0,1]$$の実数値.
- 戻り値
- 引数のHSV値に対応するRGB値(全チャンネル$$[0,1]$$の範囲)
ヒント1
x座標にcos関数,y座標にsin関数を用いる.Processingの三角関数(cos,sin,tan)の引数は度数法(度)ではなく,
弧度法(ラジアン)なので注意すること.円周率が必要ならばPIという定数が利用可能である.
球の数は可変であるため,必要な物体の数だけループしながら物体オブジェクト(Sphere)を生成して,
物体リストに追加していくこととなる.ループ変数の値をXY座標や色相にマッピングすれば所期の結果を得ることが可能である.
物体数を$$N$$とすると,ループ変数の値の範囲は$$[0,N)$$となる.これを区間$$[0,1]$$にマッピングすると上記の変換が容易となる.
ヒント2
課題EX-2. 視点を変える
前提:少なくとも「課題2-9 rayTraceメソッドを実装する」を実装していること.
任意の視点から任意の注視点を観察できるように変更する.Sceneクラスを以下のように変更し,視点を変えられるようにせよ.
class Scene
{
public ArrayList<Shape> shapes;
public ArrayList<LightSource> lightSources;
public FColor ambientIntensity;
public PVector eyePosition; // 視点位置
public PVector lookAt; // 注視点
public float screenDistance; // スクリーンまでの距離(焦点距離)
public Scene()
{
shapes = new ArrayList();
lightSources = new ArrayList();
ambientIntensity = new FColor(0.01f, 0.01f, 0.01f);
eyePosition = new PVector(0,0,-5); // デフォルトでは,本編と同じ位置から
lookAt = new PVector(0,0,0); // 原点位置を注視する(lookAtは方向を決めているだけ).
screenDistance = 5; // スクリーンまでの距離は5である.
}
public IntersectionTestResult testIntersectionWithAll(Ray ray)
{
// ..中略..
}
}
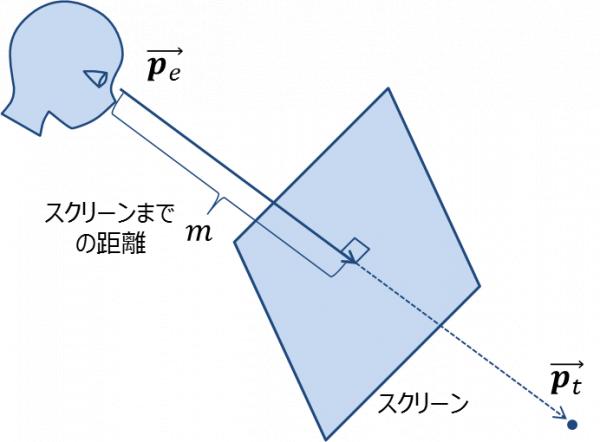
視点位置$$\vec{\bf p_{e}}$$(eyePosition),注視点$$\vec{\bf p_{t}}$$(lookAt),スクリーンまでの距離$$m$$(screenDistance)の関係は図4のようになっている.
図5は「課題3-1. 付影処理を実装する」と同じシーンを,視点位置$$(10,10,-10)$$,注視点$$(1,0,15)$$, スクリーンまでの距離$$3$$から見た例である.
ヒント1
従来の,画像座標$$(x_s,y_s)$$に対応する三次元座標$$\vec{\bf p_w}$$を計算するための変換式をよく見てみよう.
これは書き方を変えれば,以下と同じである.
この式は,X軸正方向の単位ベクトル$$\vec{\bf e_x}$$,とY軸正方向の単位ベクトル$$\vec{\bf e_y}$$を使えば 以下のようにも表現することができないか?
成分ごとに書き出してみよう.
これが何を示しているかというと,いままで$$\vec{\bf p_w}$$として使用していた変換式は,
「$$\vec{\bf p_w}$$の位置は,(原点から)X軸の方向($$\vec{\bf e_x}$$)に$$\frac{2x_s}{W-1}-1$$だけ移動し, かつY軸の方向($$\vec{\bf e_y}$$)に$$\frac{-2y_s}{H-1}+1$$だけ移動した位置である」
という意味であったと言うことである.
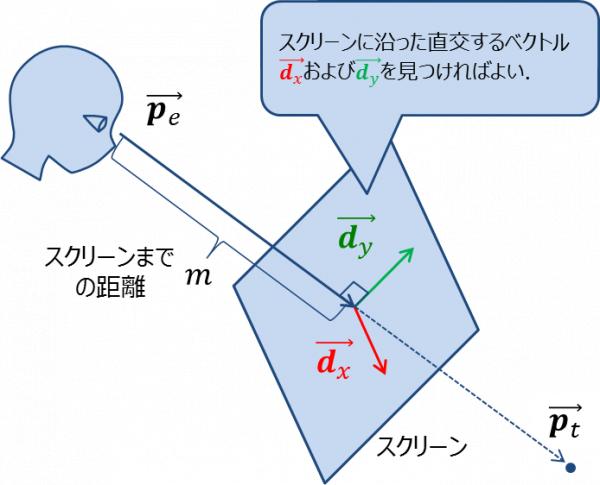
つまり,どのような位置でどのような姿勢のスクリーンであっても,スクリーンに沿った直交する一組のベクトル$$\vec{\bf d_x}$$,$$\vec{\bf d_y}$$を 見つけることができれば,$$\vec{\bf p_w}$$の位置を計算することができる,ということである(図6).
ヒント2
前述の$$\vec{\bf d_x}$$,$$\vec{\bf d_y}$$は互いに直交する.また,これらはスクリーンに沿ったベクトルであるので,どちらのベクトルも スクリーンの法線方向とも直交する.今分かっているのは,スクリーンの法線方向,すなわち視点から注視点に向かうベクトルのみである. このベクトルに直行する一組のベクトルを探さなければならない.
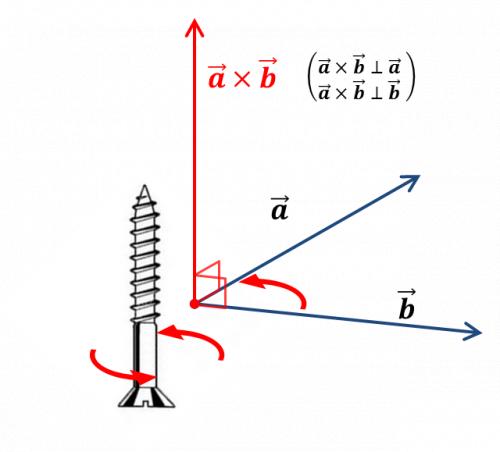
このためには,ベクトルの外積の性質を利用する.
外積の定義は以下である.
これを見ただけだとよく分からないかも知れないが,ベクトルの外積$$\vec{\bf a}\times\vec{\bf b}$$は, $$\vec{\bf a}$$とも$$\vec{\bf b}$$とも直交するベクトルとなる,という性質がある.
ベクトル$$\vec{\bf a}, \vec{\bf b}$$の外積$$\vec{\bf a}\times\vec{\bf b}$$は, 図7に示すように,ベクトル$$\vec{\bf b}$$をベクトル$$\vec{\bf a}$$に 近づけるときの右ねじの向きのベクトルとなる(左手系の場合).
この問題ではベクトルの外積計算を2回使う.かつ,決め打ちの上方向ベクトル$$\vec{\bf e_y}=(0,1,0)$$が必要となる.
ヒント3
この問題では,スクリーンの三次元空間における位置が,もともとの幅2.0高さ2.0で,中心が原点にあるXY平面上の矩形ではなくなる.
幅と高さに変化はないが,その中心は視点位置(eyePosition)から注視点(lookAt)の方向に一定距離(screenDistance)だけ離れた位置となり,
このスクリーンは視点位置から注視点に向かうベクトルに直交する.言い換えれば,視点位置から注視点に向かうベクトルがスクリーンの法線方向となる(図4).
まずは,「視点位置から注視点に向かうベクトル」を求めよう.このベクトルを$$\vec{\bf d_f}$$とすると,
となる.次にスクリーン平面に沿った一つ目のベクトル$$\vec{\bf d_x}$$を求めよう.このベクトルはスクリーンの法線方向($$\vec{\bf d_f}$$)と直交する. このベクトルを特定する方法はいくつかありうるが一番単純なのは$$\vec{\bf d_x}$$とY軸正方向の単位ベクトル$$\vec{\bf e_y}=(0,1,0)$$との外積をとることである.
スクリーン平面がどのような方向を向いているかにかかわらず$$\vec{\bf d_x}$$は,$$\vec{\bf d_f}$$の方向を見たときの右方向のベクトルとなる. そして外積の性質から$$\vec{\bf d_x}\bot\vec{\bf d_f}$$が成立する.
次に$$\vec{\bf d_y}$$を探す.このベクトルはスクリーン平面に沿ったベクトルであるので$$\vec{\bf d_y}\bot\vec{\bf d’_f}$$でなければならないし, $$\vec{\bf d_y}\bot\vec{\bf d_x}$$でなければならない.$$\vec{\bf d_y}$$が$$\vec{\bf d’_f}$$にも$$\vec{\bf d_x}$$にも直交するベクトルであるということは…?
ヒント4
$$\vec{\bf d_y}$$は$$\vec{\bf d’_f}$$と$$\vec{\bf d_x}$$の外積である.すなわち,
となる. スクリーン平面がどのような方向を向いているかにかかわらず$$\vec{\bf d_y}$$は,$$\vec{\bf d_f}$$の方向を見たときの上方向のベクトルとなる.
ここで検算をしてみよう.従来の視点位置$$\vec{\bf p_e}=(0,0,-5)$$,注視点$$\vec{\bf p_t}=(0,0,0)$$,スクリーンまでの距離$$m=5$$の場合,$$\vec{\bf d_x}$$や $$\vec{\bf d_y}$$はどのように求まるだろうか.
これを使って$$\vec{\bf d_x}$$と$$\vec{\bf d_y}$$を求めてみる.
$$\vec{\bf d_x}$$と$$\vec{\bf d_y}$$が求まった.この2つのベクトルをよく見てみよう.それぞれX軸方向の単位ベクトル,Y軸方向の単位ベクトルと一致している.
ヒント5
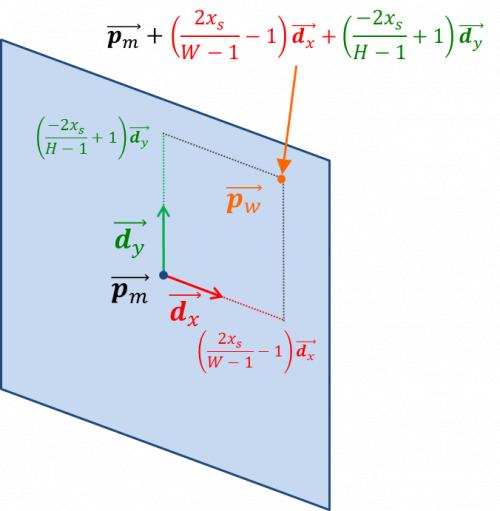
画像座標$$(x_s,y_s)$$に対応する三次元座標$$\vec{\bf p_w}$$は,スクリーンに沿った一組の互いに直交なベクトル $$\vec{\bf d_x}$$と$$\vec{\bf d_y}$$の線形和として求めることができる.
ただし,これはスクリーンが原点にある場合である.スクリーンの中心位置が$$\vec{\bf p_m}$$にある場合は以下となる(図8).
では,「スクリーンの中心位置$$\vec{\bf p_m}$$」とはいかなる位置か?ヒント3を思いだそう.
幅と高さに変化はないが,その中心は視点位置(
eyePosition)から注視点(lookAt)の方向に一定距離(screenDistance)だけ離れた位置となり, このスクリーンは視点位置から注視点に向かうベクトルに直交する.言い換えれば,視点位置から注視点に向かうベクトルがスクリーンの法線方向となる(図4).
「視点位置から注視点に向かうベクトル」とは$$\vec{\bf d’_f}$$のことである.また,視点位置は$$\vec{\bf p_e}$$であり,スクリーンまでの距離は$$m$$だった. 従って,$$\vec{\bf p_m}$$は以下となる.
全てまとめると,スクリーン上の点の三次元空間における位置$$\vec{\bf p_w}$$は以下のように表現できる.
各記号は以下である.
- $$\vec{\bf p_e}$$
- 視点位置(
eyePosition) - $$\vec{\bf p_t}$$
- 注視点の位置(
lookAt) - $$m$$
- スクリーンまでの距離
- $$\vec{\bf d_f}=\vec{\bf p_t} – \vec{\bf p_e}$$
- 視点から注視点に向かうベクトル
- $$\vec{\bf d’_f} = \frac{1}{|\vec{\bf d_f}|}\vec{\bf d_f}$$
- 正規化した$$\vec{\bf d_f}$$
- $$f_x = \frac{2x_{s}}{W-1}-1.0$$
- 正規化したX座標(変換したスクリーン座標のX成分)
- $$f_y = \frac{-2y_{s}}{H-1}+1.0$$
- 正規化したY座標(変換したスクリーン座標のY成分)
- $$x_s,y_s$$
- スクリーン座標
- $$W,H$$
- スクリーンの幅と高さ
- $$\vec{\bf d_x} = \vec{\bf e_y}\times\vec{\bf d’_f} $$
- スクリーン右方向のベクトル
- $$\vec{\bf d_y} = \vec{\bf d’_f}\times\vec{\bf d_x}$$
- スクリーン上方向のベクトル
ヒント6
課題EX-3. 画面サイズを変える
前提:「課題EX-2. 視点を変える」を実装していること.
出力画像サイズは今まで固定で512×512であった.これを任意の解像度に対応できるようにする.
Sceneクラスに以下の変更を加える.
class Scene
{
public ArrayList<Shape> shapes;
public ArrayList<LightSource> lightSources;
public FColor ambientIntensity;
public PVector eyePosition;
public PVector lookAt;
public float screenDistance;
public int width; // 出力画像の幅
public int height; // 出力画像の高さ
public Scene()
{
shapes = new ArrayList();
lightSources = new ArrayList();
ambientIntensity = new FColor(0.01f, 0.01f, 0.01f);
eyePosition = new PVector(0,0,-5);
lookAt = new PVector(0,0,0);
screenDistance = 5;
width = 512; // デフォルトでは,
height = 512; // 512x512
}
public IntersectionTestResult testIntersectionWithAll(Ray ray)
{
// ..中略..
}
}
図9は実行例である.
縦長,横長,正方形のすべての場合に対応すること.
Processing3ではsetupメソッド内でsizeメソッドを呼び出す場合,
その引数に定数しか使うことができない.
int W = 640;
int H = 480;
void setup()
{
size(W, H); // error!
}
sizeメソッドに変数を渡す必要がある場合は,以下のようにsettingsメソッド内で
行う必要がある.このメソッドはsetupメソッドよりも前に呼び出されるメソッドである.
int W = 640;
int H = 480;
void settings()
{
size(W, H); // エラーは出ない
}
void setup()
{
// size(W, H);
}
ヒント1
方法はいろいろあるが,ここでは指定された幅と高さのうち大きい方が三次元空間中の2.0の長さになるようにする.
ヒント2
指定された出力画像のサイズをチェックして,対応するスクリーン上の大きさを変数として保持する.
画像の幅を$$W$$,画像の高さを$$H$$,スクリーンの幅を$$W_{s}$$,スクリーンの高さを$$H_{s}$$とすると.
$$f_{x}$$, $$f_{y}$$は以下のように変更される.
ヒント3
余力のある方向け
スクリーンまでの距離を小さくとると画角が広くなる.
逆に画角からスクリーン距離を決めるような実装はできるだろうか.
※ カメラ(視線)のパラメータとして,視点位置,注視点,画角の三つを指定させるシステムは一般的である.
ヒント:tan
課題EX-4. 円錐を表示させる
前提:「課題2-9 rayTraceメソッドを実装する」を実装していること.
形状として円錐を実装する.
中心位置$$\vec{\bf p_c}=(c_{x}, c_{y}, c_{z})$$,高さ$$h$$,半径$$r$$の円錐の方程式は以下である(ベクトル方程式ではない)(図10).
上記の方程式と半直線$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d}$$の解析表示,
を連立してtに関する二次方程式に整理し,tについて解けばよい. ただし,これによって求まった交点と,位置$$\vec{\bf p_{\cal c}}$$とのy軸距離が$$[-h,0]$$の範囲内である場合のみ交点を持つ..
やや無理矢理だが,上記の円錐の方程式をベクトル方程式にすることもできる.
ベクトル$$\vec{\bf h}$$と,行列$${\bf M}$$は以下である.
$$i$$は虚数単位である.
この方程式と半直線の方程式$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d}$$を連立すれば交点を求めることができる.
交点$$\vec{\bf p_a}=(a_{x},a_{y},a_{z})$$における法線ベクトル$$\vec{\bf n}=(n_{x},n_{y},n_{z})$$を求めるには, 式(1)を陰関数表示にして,$$x,y,z$$の各次元で偏微分すればよい(接平面の法線ベクトルが求まる.この方法は曲面一般に使用できる.).
円錐の見た目はおおよそ図11のようになる.図11左は,位置$$\vec{\bf p_{\cal c}}=(0,-1,5)$$にある半径1.0,高さ2.0の円錐である. 図11右は,参考として「課題3-1. 付影処理を実装する」のシーンの球を円錐に置き換えたものである.
ヒント1
円錐の方程式
に半直線の方程式
を代入する.
計算を楽にするために以下を置く.
以下,$$t$$について整理していく.
$$t$$の係数を以下のように置く.
これで$$t$$に関する単純な二次方程式となる.
$$t$$の根を調べれば交点の有無と位置が分かる.
ヒント2
円錐の方程式
に半直線の方程式
を代入する.
計算を楽にするために$$\vec{\bf m} = \vec{\bf s} -\vec{\bf p_c}-\vec{\bf h}$$と置き,$$t$$について整理する.
$$t$$の係数を以下のように置く.
これで$$t$$に関する単純な二次方程式となる.
※ Processingには行列や複素数を扱う機能はないので,実装上は$$A,B,C$$はそれぞれ成分ごとの計算式に展開する必要がある(その課程で虚数単位は消えるはず).
ヒント3
「交差判定の整理」で述べたように,新たな形状(ここでは円錐)を導入するには
Shapeクラスのサブクラスを作りtestIntersectionメソッドをオーバーライドすれば良い.
円錐を表すクラスConeを導入しよう.以下のようなクラスとなる.
class Cone extends Shape
{
public PVector center;
public float radius;
public float height;
public Cone(){ this(new PVector(0,0,0), 1, 1); }
public Cone(PVector c, float r, float h)
{
center = c.copy();
radius = r;
height = h;
}
public IntersectionPoint testIntersection(Ray ray)
{
// 実装せよ.
}
}
testIntersectionメソッドを実装してこのクラスを完成させればよい.
ヒント4
余力のある方向け
この方法で表示させた円錐には底面がない.底面を表示するにはどうしたらいいだろうか.
ヒント:平面との交差判定を併用する
課題EX-5. 円柱を表示させる
前提:「課題2-9 rayTraceメソッドを実装する」を実装していること.
形状として円柱を実装する.
中心位置$$\vec{\bf p_{\cal c}}=(c_{x}, c_{y}, c_{z})$$,高さ$$h$$,半径$$r$$の円柱の方程式は以下である(ベクトル方程式ではない)(図12).
※ この式は実際は高さ無限の円柱であるため,$$h$$の値は式には出てこない.
上記の方程式と半直線$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d}$$の解析表示,
を連立して$$t$$に関する二次方程式に整理し,$$t$$について解けばよい. ただし,これによって求まった交点と,位置$$\vec{\bf p_{\cal c}}$$とのy軸距離が$$\left[-\frac{h}{2},\frac{h}{2}\right]$$の範囲内である場合のみ交点を持つ..
上記の円柱の方程式をベクトル方程式にすることもできる.
行列$${\bf M}$$は以下である.
この方程式と半直線の方程式$$\vec{\bf p}=\vec{\bf s}+t\vec{\bf d}$$を連立すれば交点を求めることができる.
交点$$\vec{\bf p_{\cal a}}=(a_x,a_y,a_z)$$における法線ベクトル$$\vec{\bf n}=(n_{x},n_{y},n_{z})$$を求めるには, 式(1)を陰関数表示にして,$$x,y,z$$の各次元で偏微分すればよい(接平面の法線ベクトルが求まる.この方法は曲面一般に使用できる.).
円柱の見た目はおおよそ図13のようになる.図13左は,位置$$\vec{\bf p_{\cal c}}=(0,0,5)$$にある半径1.0,高さ2.0の円柱である. 図13右は,参考として「課題3-1. 付影処理を実装する」のシーンの球を円柱に置き換えたものである.
ヒント1
円柱の方程式
に半直線の方程式
を代入する.
計算を楽にするために以下を置く.
以下,$$t$$について整理していく.
$$t$$の係数を以下のように置く.
これで$$t$$に関する単純な二次方程式となる.
$$t$$の根を調べれば交点の有無と位置が分かる.
ヒント2
円柱の方程式
に半直線の方程式
を代入する.
計算を楽にするために$$\vec{\bf m} = \vec{\bf s}-\vec{\bf p_c}$$と置き,$$t$$について整理する.
$$t$$の係数を以下のように置く.
これで$$t$$に関する単純な二次方程式となる.
※ Processingには行列を扱う機能はないが,$$M$$はy成分を単にゼロにする作用を持つ行列なので,少し手を加えれば上式をそのまま実装することができる.
ヒント3
「交差判定の整理」で述べたように,新たな形状(ここでは円柱)を導入するには
Shapeクラスのサブクラスを作りtestIntersectionメソッドをオーバーライドすれば良い.
円柱を表すクラスCylinderを導入しよう.以下のようなクラスとなる.
class Cylinder extends Shape
{
public PVector center;
public float radius;
public float height;
public Cylinder(){ this(new PVector(0,0,0), 1.0, 1.0); }
public Cylinder(PVector c, float r, float h)
{
center = c.copy();
radius = r;
height = h;
}
public IntersectionPoint testIntersection(Ray ray)
{
// 実装せよ
}
}
testIntersectionメソッドを実装してこのクラスを完成させればよい.
ヒント4
余力のある方向け
この方法で表示させた円柱には天井と底面がない.天井と底面を表示するにはどうしたらいいだろうか.
ヒント:平面との交差判定を併用する
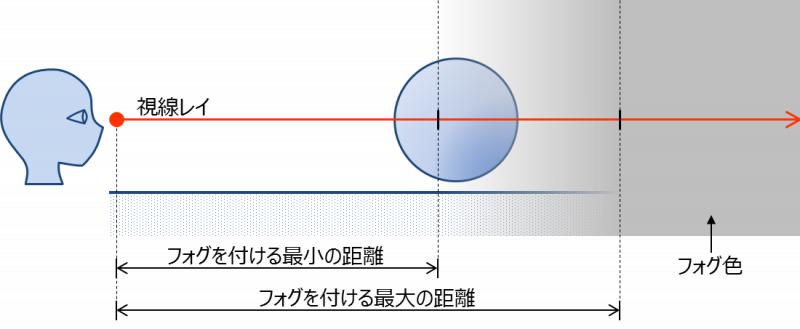
課題EX-6. フォグ
前提:「課題2-9 rayTraceメソッドを実装する」を実装していること.
フォグとは空気遠近法ともいい,遠くの物体ほど色が薄くなる表現である.フォグを使う表現では,視線と物体の交点の位置, というよりも視点から交点までの距離によって色に変化を付ける(図14).
視点から交点までの距離が一定未満である場合は通常通り放射輝度計算を行うが,その距離よりも遠くなると 交点の色をあらかじめ設定したフォグ色に近づける.そして,ある程度以上遠くなると完全にフォグ色に一致する.
フォグを使うと以下のような生成画像となる.図15左は「課題3-1. 付影処理を実装する」のシーンで フォグを付ける最小の距離を10,最大の距離を30,フォグ色を灰色とした場合の出力画像である.図15右同じシーンでフォグ色を背景色と一致させた例である.
このフォグの機能を実装せよ.
ヒント1
フォグを実装する場合,交点の位置で計算された色とフォグ色とで線形補間を行うのが最も簡単な実現方法である(もちろん他の補間方法もあり得る).
フォグを考慮した出力色(放射輝度)$$R’_{r}$$は以下のように計算すればよい.
各記号は以下である.
- $$R_r$$
- 交点の位置で計算された放射輝度
- $$R_{fog}$$
- フォグ色
- $$\vec{\bf p_a}$$
- 視線と物体の交点位置
- $$\vec{\bf p_e}$$
- 視点位置
- $$g_{near}$$
- フォグをつける最小の距離
- $$g_{far}$$
- フォグをつける最大の距離
ヒント2
Sceneクラスに以下のような変更を加え,rayTraceメソッドでこれらを使用する.
class Scene
{
public ArrayList<Shape> shapes;
public ArrayList<LightSource> lightSources;
public FColor ambientIntensity;
public boolean useFog; // フォグを使うかどうか
public float fogNear; // フォグをつける最小の距離
public float fogFar; // フォグをつける最大の距離
public FColor fogColor; // フォグに使う色
public Scene()
{
shapes = new ArrayList();
lightSources = new ArrayList();
ambientIntensity = new FColor(0.01f, 0.01f, 0.01f);
useFog = false; // デフォルトではフォグを使わない.
fogNear = 0; // 距離はどちらも,
fogFar = 0; // とりあえず0にしておく.
fogColor = new FColor(0); // 色も黒にしておく.
}
// ..以下略..
ヒント3
課題EX-7. トゥーンシェーディング
前提:「課題2-9 rayTraceメソッドを実装する」を実装していること.
トゥーンシェーディングとは,陰影を意図的に不連続にしたセルアニメのようなシェーディングである. 例えば図16のような表現である.
このトゥーンシェーディングを実装せよ.
ヒント1
この課題は二つの機能の合成である.
- 陰影を離散化する
- 拡散反射光の輝度も鏡面反射光の放射輝度もベクトルの内積に依存していることを利用する.
- ベクトルの内積の値を離散化すると不連続な陰影を得ることができる.
- 輪郭をつける
- 交点が物体の輪郭に近いときに一定の色を算出するようにすればよい.
- 輪郭に近いかどうかは,面の法線ベクトルと視線ベクトルのなす角を利用する.
ヒント2
連続的な値を離散化する方法はいくつかある.例えば以下のような式が使える.
拡散反射光や鏡面反射光の計算に使う内積の値を$$A$$とする.トゥーンシェーディングを実現するために加工した$$A$$の値を$$A’$$とすると,以下のようになる.
各記号は以下である.
- $$N_t$$
- 陰影の段階の数(たとえば3なら三段階の陰影となる)
- $$\lceil x \rceil$$
ceil関数.$$x$$以下で最も大きい整数を返す.- $$cos^{-1}(x)$$
- 余弦関数の逆関数(
acos関数)
ヒント3
面の法線ベクトルと視線ベクトルのなす角が90度に近いとき輪郭であるとしてあつかえばよい(図17).
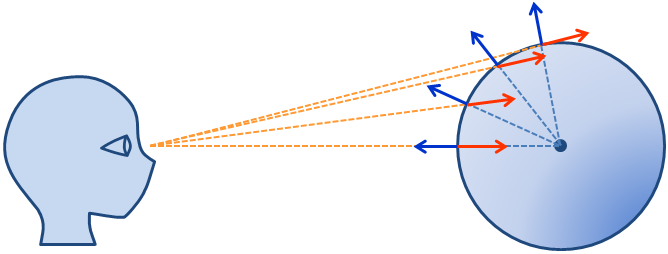
図17. 法線ベクトルと視線ベクトル
このために面の法線ベクトルと視線ベクトルのなす角を直接求めてもよいが,この2つのベクトルの内積を利用するのが簡単である. 輪郭を考慮した放射輝度(色)$$R’_r$$の計算は以下のようになる.
各記号の意味は以下である.
- $$R_r$$
- 交点の位置で計算された放射輝度
- $$R_t$$
- 輪郭の色
- $$q$$
- 輪郭の太さ(内積値のしきい値)
- $$\vec{\bf n}$$
- 面の法線方向ベクトル(ただし,$$\left|\vec{\bf n}\right| \le 1$$)
- $$\vec{\bf d_e}$$
- 視線方向ベクトル(ただし,$$\left|\vec{\bf d_e}\right| \le 1$$)
ヒント4
Sceneクラスに以下のような変更を加え,rayTraceメソッドでこれらを使用する.
class Material
{
public FColor ambientReflectance;
public FColor diffuseReflectance;
public FColor specularReflectance;
public float shininess;
public boolean useToon; // トゥーンシェーディングを使うかどうか
public int toonLevel; // 陰影の段階
public float toonEdgeThickness; // 輪郭の太さ
public FColor toonEdgeColor; // 輪郭の色
public Material()
{
ambientReflectance = new FColor(0.01f, 0.01f, 0.01f);
diffuseReflectance = new FColor(0.69f, 0.69f, 0.69f);
specularReflectance = new FColor(0.30f, 0.30f, 0.30f);
shininess = 8;
useToon = false; // デフォルトではトゥーンシェーディングを使用しない.
toonLevel = 0; // その他のパラメータも
toonEdgeThickness = 0; // とりあえず
toonEdgeColor = new FColor(0); // ゼロにしておく.
}
}











0 Comments.