The Textbook of RayTracing @TDU

[—ATOC—] 1 [—AUTO_SECTION_NUMBER—] 1

物体表面の色

前章では三つの反射係数$$k_{a}, k_{d}, k_{s}$$を使用した．反射係数（反射率）は入射した光に対する反射する光の比率である．たとえば，入射した光の量が1.0で反射した光の量が0.7であれば反射係数は$$\frac{0.7}{1.0}=0.7$$となる．

現実の物体表面では，反射係数（反射率）は入射した光の波長によって異なる．
たとえば（極端な例であるが）ある物体表面において，波長700nmの光の反射率が1.0で，それ以外の波長の反射率が0.0ならばその物体は赤く見える(図1)．

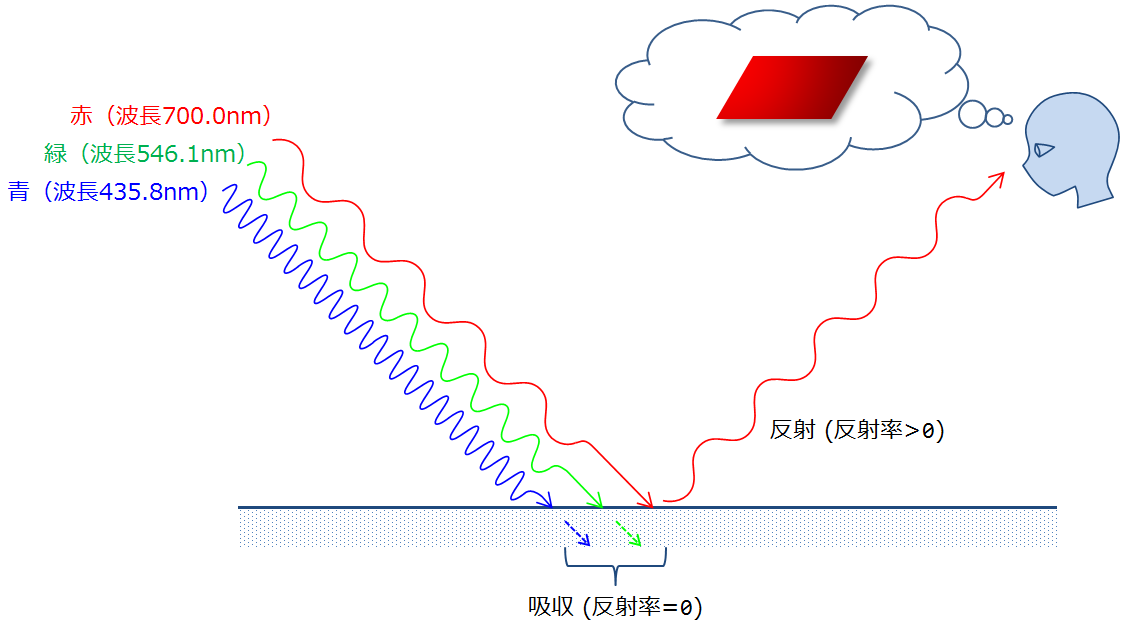
図1. 波長ごとに反射率は異なる

前章の実装では反射係数$$k_{a}, k_{d}, k_{s}$$が登場したが，レイトレーシング法において 物体表面の色を再現するには，これら反射係数をRGB各チャネルごとに定義する必要がある．

また，光源の照度$$E_{i}$$も環境光の照度$$E_{a}$$も単一の値として処理していた．
色の付いた光を再現するには照度も同様にRGB各チャネルごとに定義する必要がある．

複数の光源

前章では，光源を一つに限定していた．

Phongの反射モデルでは，物体表面の反射光の輝度を以下のように表現すると述べた．

• $$L_{a}$$：環境光の反射光の輝度
• $$L_{d}$$：直接光の拡散反射光の輝度
• $$L_{s}$$：直接光の鏡面反射光の輝度

Phongの反射モデルは本来複数の光源を考慮している．本来の式は以下である．

• $$L_{a}$$：環境光の反射光の輝度
• $$L^{i}_{d}$$：i番目の光源からの直接光の拡散反射光の輝度
• $$L^{i}_{s}$$：i番目の光源からの直接光の鏡面反射光の輝度

物体表面の放射輝度は，シーンの環境光と，シーンに存在する全ての光源からの光の反射光の総和となっている．

プログラムの整理と拡張

前章までのプログラムでは様々な情報を個々のローカル変数として保持しており，また処理をほとんどすべてmain関数内に詰め込んでいたため機能拡張が困難である．

本節では，以下の機能を加えるために前節までのプログラムを整理する．

• 3チャネル(RGB)の色への対応
• 複数の物体（球 or 平面）への対応
• 複数の光源への対応

データ型を定義する

球や光源など，論理的に異なる実体は個々に構造体として定義した方が便利である． そこで，以下のデータを保持するための構造体を定義する．

• 色
• レイ
• 形状(球 or 平面)
• 物体の質感
• 光源(点光源 or 平行光源)
• シーン

色 – colorf_t構造体

colorf_t構造体はRGB値を実数型で保持する．

typedef struct
{
  float r,g,b;
} colorf_t;

この構造体は，光源の色と反射係数として用いる．

レイ – ray_t構造体

ray_t構造体は半直線の情報，すなわち始点の位置ベクトル(start)と 方向ベクトル(direction)を保持する．

typedef struct
{
  vector_t start;     /* 始点 */
  vector_t direction; /* 方向ベクトル */
} ray_t;

形状 – sphere_t, plane_t, shape_t構造体

sphere_t構造体は球の情報，すなわち中心の位置ベクトル(center)と 半径(radius)を保持する．

typedef struct
{
  vector_t center; /* 球の中心 */
  float radius;    /* 球の半径 */
} sphere_t;

plane_t構造体は平面の情報，すなわち面の法線ベクトル(normal)と その面が通る点の位置ベクトル(position)を保持する．

typedef struct
{
  vector_t normal;   /* 法線ベクトル */
  vector_t position; /* 面が通る点の位置ベクトル */
} plane_t;

shape_t構造体は，sphere_t構造体とplane_t構造体を束ねる型であり， 内部では共用体を使って球と平面のどちらかの情報を保持する．

shape_type列挙型のメンバ(type)が，球と平面のどちらの情報が保持されているかを示している．

また後述のmaterial_t構造体型のメンバがあり，これはその物体の表面の質感を表す情報を保持している．

typedef enum 
{ 
  ST_SPHERE, /* 球 */
  ST_PLANE,  /* 平面 */
 } shape_type; 

typedef struct
{
  shape_type type;     /* 球 or 平面 */
  union
  {
    sphere_t sphere;   /* 球の情報 */
    plane_t plane;     /* 平面の情報 */
  } data;

  material_t material; /* 物体表面の質感 */
} shape_t;

物体表面の質感 – material_t構造体

material_t構造体は，物体表面の質感，すなわち前節で登場した反射係数の 組($$k_{a},k_{d},k_{s}$$)と光沢度を保持する．

それぞれの反射係数がcolorf_t構造体で保持されている点に注意せよ． 前節で説明したように，反射係数をRGBの各チャンネルごとに定義することで物体表面に色をつけることが可能となる．

typedef struct
{
  colorf_t ambient_ref;   /* 環境光反射率(RGB) */
  colorf_t diffuse_ref;   /* 拡散反射率(RGB) */
  colorf_t specular_ref;  /* 鏡面反射率(RGB) */
  float shininess;        /* 光沢度 */
} material_t;

光源 – light_t構造体

light_t構造体は光源の情報を保持する． light_type列挙型のメンバ(type)が，光源が点光源であるか平行光源であるかを示している． 点光源と平行光源については5-1.1.3. 光源を参照せよ．

vectorメンバは，その光源が点光源ならば光源の位置，その光源が平行光源であるならば光源の方向ベクトルである．

光源の強さもcolorf_t構造体で定義されている点に注意せよ．これによって 光源に色を持たせることが可能となる．

typedef enum 
{ 
  LT_POINT,       /* 点光源 */
  LT_DIRECTIONAL, /* 平行光源 */
} light_type;

typedef struct
{
  light_type type;      /* 点光源 or 平行光源 */
  vector_t vector;      /* 光源位置 or 光線方向 */
  colorf_t illuminance; /* 照度(RGB) */
} light_t;

シーン – scene_t構造体

scene_t構造体はシーン，つまり空間中に存在する物体や光源のセットを保持する構造体である．

shapesメンバは，シーン中の物体を表す．lightsメンバはシーン中の光源を表す．
どちらもポインタとして定義されていることに注意せよ．実際にデータを格納する前にはmalloc関数でメモリ領域を確保する必要がある．

typedef struct
{
  shape_t *shapes;              /* 物体リストへのポインタ */
  size_t num_shapes_capacity;   /* 物体リストの最大格納数 */
  size_t num_shapes;            /* 物体リストに実際に格納されている数 */
  light_t *lights;              /* 光源リストへのポインタ */
  size_t num_lights_capacity;   /* 光源リストの最大格納数 */
  size_t num_lights;            /* 光源リストに実際に格納されている数 */
  colorf_t ambient_illuminance; /* 環境光の強さ(RGB) */
} scene_t;

処理を関数に切り出す

交差判定や光線追跡などを個々に関数として切り出すことでプログラム全体の見通しをよくする．

交差判定(レイと単一の物体) – intersection_test関数

intersection_test関数は，レイと単一の物体との交差判定を行う． 交点が存在する場合は，その点への距離と位置と，その位置での法線ベクトルを返す．

int intersection_test(
    const shape_t *shape,           /* 【入力】物体(球 or 平面) */
    const ray_t* ray,               /* 【入力】レイ */
    intersection_point_t* out_intp  /* 【出力】交点などの情報 */
);

• shape
  • 【入力】交差判定の対象のshape_t構造体へのポインタ．
• ray
  • 【入力】交差判定の対象のray_t構造体へのポインタ．
• out_intp
  • 【出力】交点などの情報を出力するための後述のintersection_point_t構造体へのポインタ．NULLでもよい．
• 戻り値
  • rayが表す半直線上にshapeとの交点が存在しない場合はゼロを返す．交点が存在する場合は非ゼロを返す．

intersection_point_t構造体は，交点までの距離，交点の位置ベクトル，交点における物体表面の法線ベクトルの情報を保持する構造体である．

typedef struct
{
  float distance;       /* 交点までの距離 */
  vector_t position;    /* 交点の位置ベクトル */
  vector_t normal;      /* 交点における物体表面の法線ベクトル */
} intersection_point_t;

交差判定(レイとシーン内の全ての物体) – get_nearest_shape関数

get_nearest_shape関数は，レイとシーンに含まれる全ての物体との交差判定を行う． 交点が存在する場合は，最も近い物体へのポインタと，それとの交点への距離と位置と，その位置での法線ベクトルを返す．

int get_nearest_shape(
    const scene_t* scene,            /* 【入力】交差判定対象のシーン */
    const ray_t *ray,                /* 【入力】交差判定の対象のレイ */
    float max_dist,                  /* 【入力】交差判定の最大距離 */
    int exit_once_found,             /* 【入力】交差が一つでも見つかった場合に直ちに判定処理を終了するか否か */
    shape_t **out_shape,             /* 【出力】レイに最も近い物体へのポインタ */
    intersection_point_t *out_intp   /* 【出力】最も近い物体との交点などの情報*/
);

• scene
  • 【入力】交差判定の対象のscene_t構造体へのポインタ．
• ray
  • 【入力】交差判定の対象のray_t構造体へのポインタ．
• max_dist
  • 【入力】交差判定の最大距離．この距離より遠い位置で交点が見つかった場合は無視する．無限遠として処理する場合にはFLT_MAXを使用する．
• exit_once_found
  • 【入力】交差が一つでも見つかった場合に直ちに判定処理を終了するか否か．(非0で判定を終了．0で継続．)
• out_shape
  • 【出力】交点が存在する最も近いshape_t構造体へのポインタ．NULLでもよい．
• out_intp
  • 【出力】交点などの情報を出力するためのintersection_point_t構造体へのポインタ．NULLでもよい．
• 戻り値
  • scene中に，rayが表す半直線上に交差する物体が存在しない場合はゼロを返す．そうでない場合は非ゼロを返す．

光線追跡 – raytrace関数

raytrace関数は与えられたシーンにおける，単一のレイでの光線追跡を行い，その点での色を返す．

int raytrace(
    const scene_t* scene,   /* 【入力】交差判定対象のシーン */
    const ray_t *eye_ray,   /* 【入力】交差判定の対象のレイ */
    colorf_t *out_col       /* 【出力】光線追跡結果の色(輝度値) */
);

• scene
  • 【入力】交差判定の対象のscene_t構造体へのポインタ．
• ray
  • 【入力】交差判定の対象のray_t構造体へのポインタ．
• out_col
  • 【出力】光線追跡の結果の色（輝度値）を格納するためのcolorf_t構造体へのポインタ．NULLは不可．
• 戻り値
  • rayが表すレイと交差する物体が存在しない場合はゼロを返す．そうでない場合は非ゼロを返す．

main関数

以上を用いるとmain関数を以下のように簡略化できる．レンダリング処理はraytrace関数に追い出したため， main関数をこれ以上変更する必要はなくなった．

void scene_setting(scene_t *scene); /* forward */

int main()
{
  int y,x;                            /* スクリーン座標 */
  unsigned char r,g,b;                /* 画素値(RGB) */
  scene_t scene;
  vector_t eye_pos    = { 0, 0, -5 }; /* 視点位置 */
  vector_t pw;                        /* 三次元空間でのスクリーン座標 */

  scene_setting(&scene); /* シーン設定 */
  
  printf("P3n");
  printf("%d %dn", WIDTH, HEIGHT);
  printf("255n");

  pw.z = 0; 
  
  for(y = 0; y < HEIGHT; ++y)
    {
      pw.y = (-2.0f * y)/(HEIGHT-1) + 1.0f;
      for(x = 0; x < WIDTH; ++x)
        {
          ray_t eye_ray;
          colorf_t col = {100/255.0, 149/255.0, 237/255.0}; /* 背景色 */
          
          pw.x = (2.0f * x)/(WIDTH-1 ) - 1.0f;

          eye_ray.start = eye_pos;
          eye_ray.direction.x = pw.x - eye_pos.x;
          eye_ray.direction.y = pw.y - eye_pos.y;
          eye_ray.direction.z = pw.z - eye_pos.z;

          raytrace(&scene, &eye_ray, &col); /* レイトレース */

          r = 255 * CLAMP(col.r, 0, 1);
          g = 255 * CLAMP(col.g, 0, 1);
          b = 255 * CLAMP(col.b, 0, 1);

          printf("%d %d %dn", r, g, b);
          
        }/* for */
    }/* for */

  free(scene.lights);
  free(scene.shapes);

  return 0;
  
}/* int main() */
&#91;/c&#93;</div>

<h4>シーンの設定 - scene_setting関数</h4>

<p>前述のmain関数内に<strong>scene_setting関数</strong>が登場した．この関数は，scene_t構造体にシーンの情報を書き込むヘルパー関数である．</p>

<div>
void scene_setting(scene_t *scene);

重要なことはシーンの内容を変更するだけならばscene_setting関数の内容を変更するだけで実現することができる，ということである．

つまりscene_setting関数を，main関数とは別の翻訳単位──例えばscene_setting.c──に保存しておけば，シーンを変更しても scene_setting.cのみを再コンパイルし他のオブジェクトファイルと再リンクするだけで実行形式を生成することができる．

このようなビルドプロセスを実現するためには通常makeを使用する(次節)．

makeを使う

いままでは，プログラムをビルドするためにgccを直接起動していたが，この方法ではプログラムオプションなどをいちいち手動で指定する必要があり面倒である．
また，本章のプログラムからはソースファイルが多数ありビルド手順が複雑であるため，makeコマンドを使用する．

makeコマンドは，Makefileと呼ばれるファイルに記述されたプログラムの構築方法を実行するコマンドである．
makeはソースファイルが変更された場合は変更のあったソースファイルのみ処理する，といったことを自動的に行ってくれる．

Makefileは以下のような生成規則のリストで記述される．

「それを構築するためのコマンド」の直前(上の      の部分)は必ずタブ文字一つである点に注意すること．

たとえば，課題2-1では以下のようなコマンドで実行形式を生成した．

この生成をMakefileで定義するには，以下のように記述する．

ただし，通常はこのように.Cファイルから直接に実行形式を生成することはしない．

通常プログラムは複数のソースファイルで構成される． この場合プログラムを構成するソースファイル群をコンパイルし，その結果生成されたオブジェクトファイル群をリンクすることで実行形式の生成を行う(図2)．

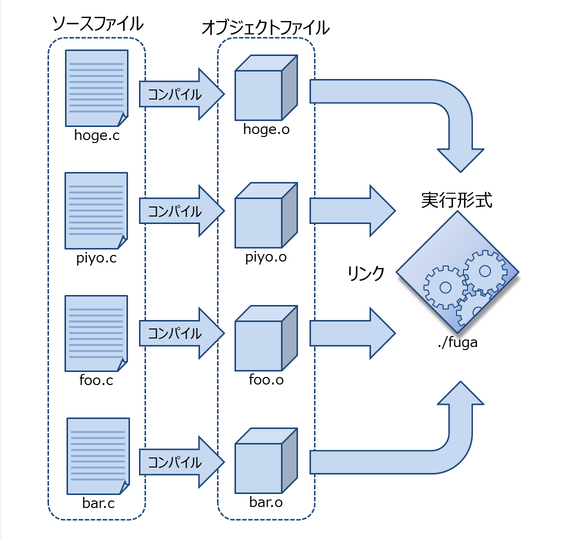
図2. 通常のビルドプロセス

オブジェクトファイル(gccでは.oという拡張子を持つ)は，ソースコードをコンパイルし実行形式にする前の中間形式である．

ソースコードを一部のみを変更した場合は，変更したソースファイルのみをコンパイルし，他は生成済みのオブジェクトファイルを使って実行形式を生成する(図3)．

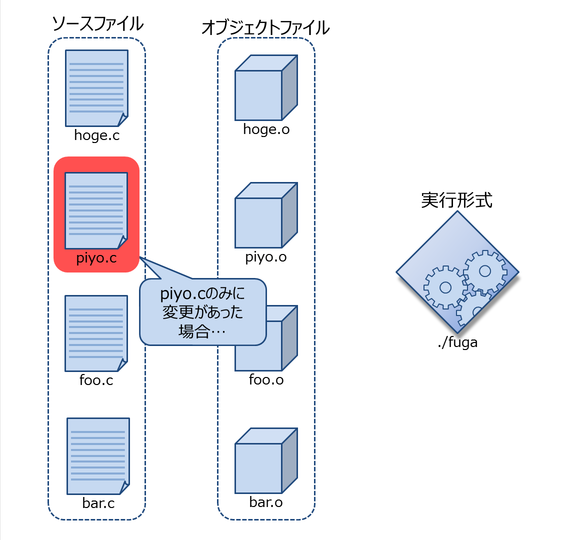
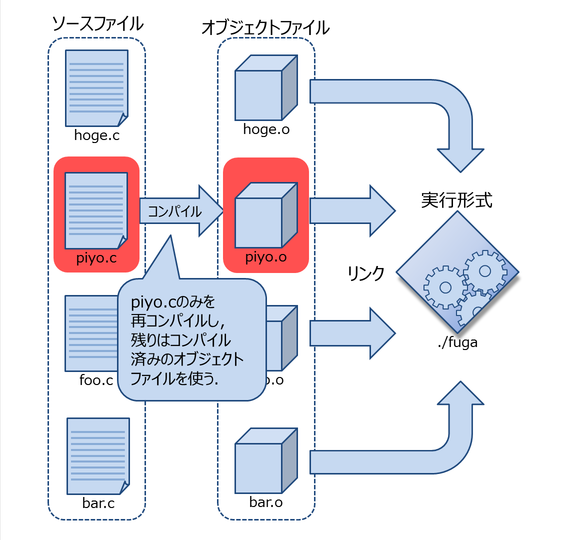
図3. 変更のあったファイルのみを再コンパイルすればよい

これを実現するためMakefileは通常以下のように書く．

$^は構築対象に必要なファイル(コロンの右側)，$@は構築対象のファイル名(コロンの左側)に展開される定義済みの変数である．
実行形式diffuse_onlyを生成するためには以下のコマンドを用いる．

こうしておけば，例えばvector_utils.cは変更しておらず，diffuse_only.cのみを変更した場合には， diffuse_only.cのみが再コンパイルされ，実行形式が生成される．

上の例で4行目と6行目の生成規則にコマンドが記述されていないことに注目せよ．
この部分は1～2行目のパターンルールによって実行するべきコマンドが定義されている．

「%.o : %.c」は「.cファイルから.oファイルを作る」ということを意味している．
vector_utils.oやdiffuse_only.oはこのパターンルールに定義されたコマンドを使って生成される．

makeについてのより詳しい説明は以下を参照せよ．
GNU `make’

課題 [—EXCLUDE—]

課題2-3. raytrace関数を実装する

以下をダウンロードしraytarce関数を実装せよ．

raytracing_tk_ch6.tar.gz

このアーカイブには以下の7つのファイルが含まれている．

• Makefile
  • Makefile．この課題では変更する必要はない．
• main.c
  • main関数．この課題では変更する必要はない．
• raytracing.h
  • 本節で解説した構造体の定義と関数の宣言．この課題では変更する必要はない．
• raytracing.c
  • intersection_test関数，get_nearest_shape関数，raytrace関数の定義が含まれる．このファイルを変更する．
• vector_utils.c
  • ベクトルを扱うための関数の定義．この課題では変更する必要はない．
• vector_utils.h
  • ベクトルを扱うための構造体の定義と関数の宣言．この課題では変更する必要はない．
• scene_settings1.c
  • scene_setting関数の定義．この課題では変更する必要はない．

生成画像は図4のようになる．

図4. scene1の生成画像

プログラムのビルド方法および実行方法

以下のコマンドでプログラムの実行形式および画像を生成する．

以下のコマンドで生成結果を確認する．

ヒント0

int raytrace(const scene_t* scene, const ray_t *eye_ray, colorf_t *out_col)
{
  /*1. 視線方向(eye_ray)の方向でもっとも近い物体を探す。*/

  if (/*視線方向に物体があった場合*/)
  {
     colorf_t col = {0,0,0}; /*色の計算結果を入れる変数*/

     /*2. 環境光の強さを計算してcolに入れる。 */

     for(/*3. すべての光源について処理する*/)
     {
         /*4. 入射ベクトルを計算する（点光源の場合と平行光源の場合）。*/

         /*5. 拡散反射光を計算してcolに足し合わせる。*/

         /*6. 鏡面反射光を計算してcolに足し合わせる*/
     }

     *out_col = col;

     return 1;
  }
  else /*視線方向に物体がなかった場合*/
  {
     return 0;
  }
}/* int raytrace(const scene_t* scene, const ray_t *eye_ray, colorf_t *out_col) */

ヒント0.1

int raytrace(const scene_t* scene, const ray_t *eye_ray, colorf_t *out_col)
{
  /*1. 視線方向(eye_ray)の方向でもっとも近い物体を探す。*/
  int res;
  shape_t *shape;
  intersection_pint_t intp;
  res = get_nearest_shape(scene, eye_ray, FLT_MAX, 0, &shape, &intp);

  if ( res /*視線方向に物体があった場合*/)
  {
     colorf_t col = {0,0,0}; /*色の計算結果を入れる変数*/

     /*2. 環境光の強さを計算してcolに入れる。 */

     for(/*3. すべての光源について処理する*/)
     {
         /*4. 入射ベクトルを計算する（点光源の場合と平行光源の場合）。*/

         /*5. 拡散反射光を計算してcolに足し合わせる。*/

         /*6. 鏡面反射光を計算してcolに足し合わせる*/
     }

     *out_col = col;

     return 1;
  }
  else /*視線方向に物体がなかった場合*/
  {
     return 0;
  }
}/* int raytrace(const scene_t* scene, const ray_t *eye_ray, colorf_t *out_col) */

ヒント１

ヒント２

課題2-4. 床を付ける(scene_setting関数)

課題2-3のソースコードのscene_setting1.cをコピーしてscene_setting関数を変更し， シーンに平面を追加せよ．

• 平面の法線：$$\vec{\bf n}=(0,1,0)$$
• 平面が通る点：$$\vec{\bf p}=(0,-1,0)$$
• 反射係数は好きに設定して良い
  • 例として，ここでは以下とする．
    • 環境光反射係数：$$k^{RGB}_{a}=(0.01,0.01,0.01)$$
    • 拡散反射係数：$$k^{RGB}_{d}=(0.69,0.69,0.69)$$
    • 鏡面反射係数：$$k^{RGB}_{s}=(0.3,0.3,0.3)$$
    • 光沢度：$$\alpha=8$$

手順は以下である．

1. scene_setting1.cをscene_setting2.cというファイル名でコピーする．

   $ cp scene_setting1.c scene_setting2.c
2. scene_setteing2.cのscene_setting関数を書き換える．

3. Makefileに以下を書き加える．

   scene2$(EXESUF) : scene_setting2.o $(OBJS)
         $(LD) $(LDFLAGS) $^ -o $@
   $(LD)の前はタブ文字であることに注意せよ.Makefile内には同様の記述があるのでそれをコピーして用いればよい(ファイル先頭などに追記してしまうとうまくいかない)．

生成画像は図5のようになる．

図5. scene2の生成画像

プログラムのビルド方法および実行方法

以下のコマンドでプログラムの実行形式および画像を生成する．

以下のコマンドで生成結果を確認する．

ヒント

課題2-5. ランダムに球を100個配置する

課題2-4のソースコードのscene_setting2.cをコピーしてscene_setting関数を変更し， シーンにランダムに球を100個配置せよ．

• 平面
  • 課題2-4と同じ
• 球の分布範囲
  • 球の半径:$$\displaystyle radius=\{ r: 0.25 \leq r \leq 0.5 \}$$
  • 球の中心:$$\vec{\bf p_{\cal c}}=(c_{x}, c_{y}, c_{z})$$
    • $$c_{x}=\{x: -2.5 \leq x \leq 2.5 \}$$
    • $$c_{y}=\{y: 0.0 \leq y \leq 2.0 \}$$
    • $$c_{z}=\{z: 0.0 \leq z \leq 20.0 \}$$
  • マテリアル
    • 環境光反射係数:$$k^{RGB}_{a}=(0.1,0.1,0.1)$$
    • 拡散反射係数：$$k^{RGB}_{d}=(k^{R}_{d},k^{G}_{d},k^{B}_{d})$$
      • $$k^{R}_{d}=\{r: 0.5 \leq r \leq 1.0\}$$
      • $$k^{G}_{d}=\{g: 0.5 \leq g \leq 1.0\}$$
      • $$k^{B}_{d}=\{b: 0.5 \leq b \leq 1.0\}$$
    • 鏡面反射係数：$$k^{RGB}_{s}=(k^{R}_{s},k^{G}_{s},k^{B}_{s})$$
      • $$k^{R}_{s}=\{r: 0.3 \leq r \leq 0.5\}$$
      • $$k^{G}_{s}=\{g: 0.3 \leq g \leq 0.5\}$$
      • $$k^{B}_{s}=\{b: 0.3 \leq b \leq 0.5\}$$

手順は以下である．

1. scene_setting2.cをscene_setting3.cというファイル名でコピーする．

   $ cp scene_setting2.c scene_setting3.c
2. scene_setteing3.cのscene_setting関数を書き換える．

3. Makefileに以下を書き加える．

   scene3$(EXESUF) : scene_setting3.o $(OBJS)
         $(LD) $(LDFLAGS) $^ -o $@
   $(LD)の前はタブ文字であることに注意せよ.Makefile内には同様の記述があるのでそれをコピーして用いればよい(ファイル先頭などに追記してしまうとうまくいかない)．

生成画像は図6のようになる．
以下はランダムシードを固定値125とした場合の結果である．ただし，乱数をとる 順序によっては必ずしもこの結果と同じにはならない(結果が異なってもあまり気にしないこと)．

図6. 生成画像

プログラムのビルド方法および実行方法

以下のコマンドでプログラムの実行形式および画像を生成する．

以下のコマンドで生成結果を確認する．

ヒント

#include <stdlib.h>

int rand(void);
void srand(unsigned int seed);

srand(time(NULL));

srand(123);

rand(); /* 引数なしで単に呼び出せばよい． */

float f;
f = (float)rand()/RAND_MAX;

float f;
f = a + (b-a) * (float)rand()/RAND_MAX;