The Textbook of RayTracing @TDU

[—ATOC—] 1 [—AUTO_SECTION_NUMBER—] 1

完全鏡面反射

鏡やクロム球の表面などで，入射した光がほぼ完全に反射する現象を完全鏡面反射という(図1)．

完全鏡面反射する面では，他の物体の表面で反射した光が見えていると言える(図2)．

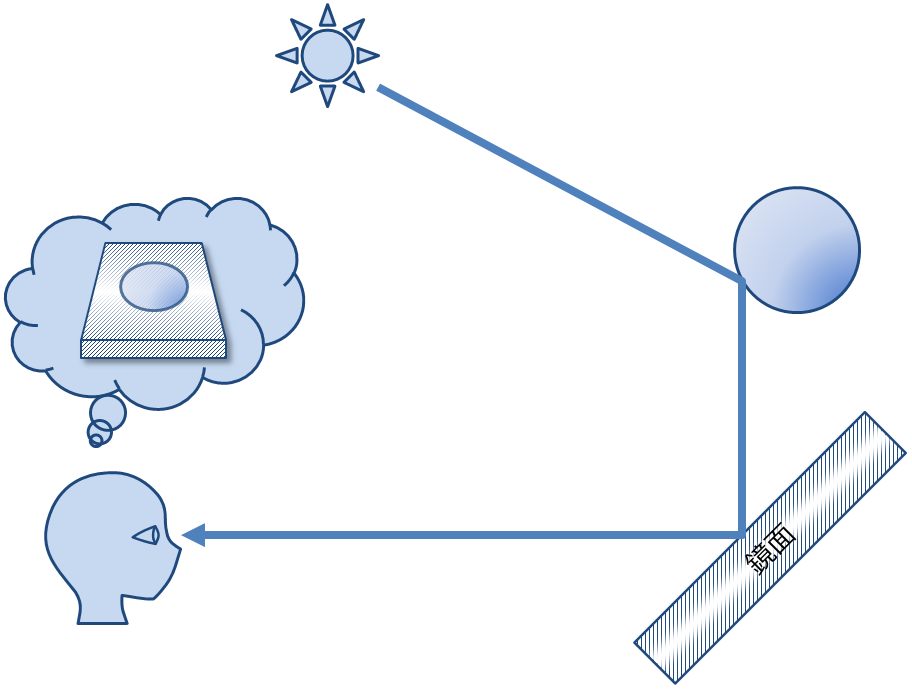
図2. 他の物体の表面で反射した光が見えている

これをレイトレーシング法で再現することは容易である．完全鏡面反射する表面を再現するには，物体表面の色を決める処理の中で視線と物体の交点を， 仮想的な視点としてレイトレーシングを行えばよい(図3)．

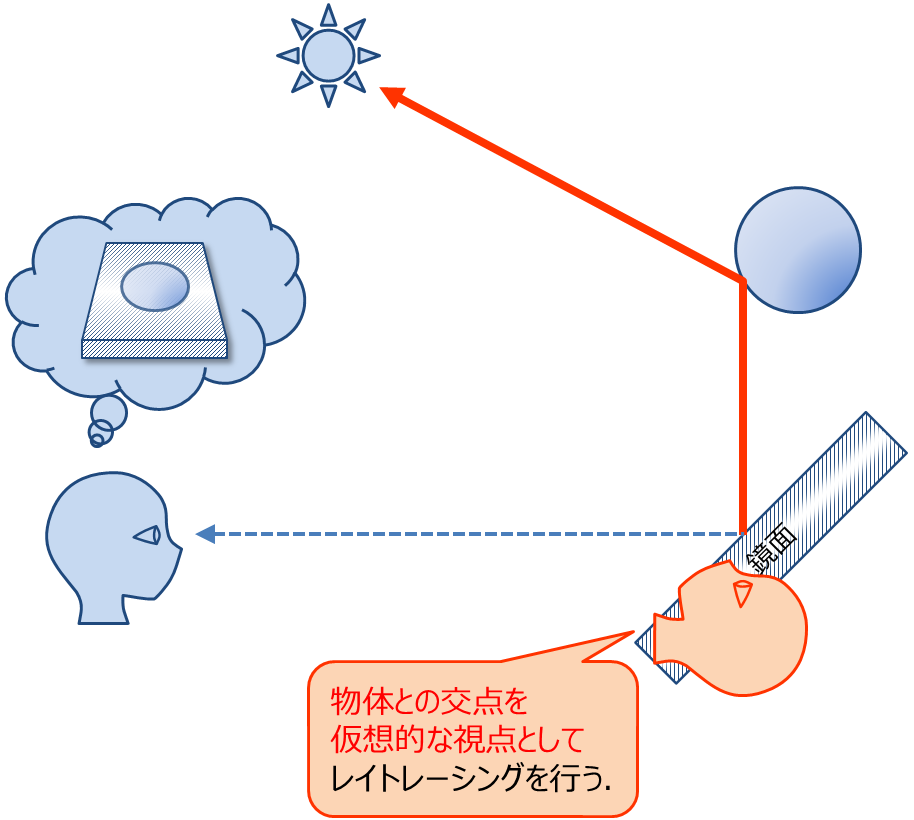
図3. 完全な鏡面の再現

この仮想的な視点の位置と視線方向は以下のようになる．

• 仮想的な視点の位置
  • 物体と(大元の)視線との交点$$\vec{\bf p_{\cal i}}$$
• 仮想的な視点の視線方向
  • (大元の)視線方向の，交点$$\vec{\bf p_{\cal i}}$$における正反射ベクトル$$\vec{\bf r_{\cal e}}=2\left(\vec{\bf n}\cdot\vec{\bf v}\right)\vec{\bf n}-\vec{\bf v}$$
    • $$\vec{\bf n}$$：交点$$\vec{\bf p_{\cal i}}$$における法線ベクトル
    • $$\vec{\bf v}$$：(大元の)視線ベクトルの逆ベクトル

物体表面の輝度$$L_{r}$$を以下のように変更する．

• $$L_{a}$$：環境光の反射光の輝度
• $$L^{i}_{d}$$：i番目の光源からの直接光の拡散反射光の輝度
• $$L^{i}_{s}$$：i番目の光源からの直接光の鏡面反射光の輝度
• $$L_{f}$$：完全鏡面反射光の輝度

また，完全鏡面反射光の輝度$$L_{f}$$は以下である．

• $$k_{f}$$：完全鏡面反射係数
• $$L_{re}$$：(前述の)$$\vec{\bf r_{\cal e}}$$方向で得られる輝度

完全鏡面反射の実装

仮想的な視点の位置と方向

7-2.2. シャドウレイと同様に始点位置に注意する．
（大元の）視線ベクトルと物体の交点をそのままレイの始点として使用するとうまくいかない(説明省略)．

material構造体の変更

前節の完全鏡面反射の対応のため，material構造体に変更を加える．

typedef enum 
{ 
  MT_DEFAULT,       /* 通常の質感 */
  MT_PERFECT_REF,   /* 完全鏡面反射を使用する */
} material_type;

typedef struct
{
  colorf_t ambient_ref;   /* 環境光反射率(RGB) */
  colorf_t diffuse_ref;   /* 拡散反射率(RGB) */
  colorf_t specular_ref;  /* 鏡面反射率(RGB) */
  float shininess;        /* 光沢度 */

  material_type type;     /* マテリアルタイプ */
  colorf_t reflect_ref;   /* 完全鏡面反射光係数(RGB) */

} material_t;

• type
  • 質感のタイプを指定する．
    • MT_DEFAULTなら通常の(完全鏡面反射を使用しない)質感
    • MT_PERFECT_REFなら完全鏡面反射を使用する質感
• reflect_ref
  • 完全鏡面反射光係数を指定する．

わざわざ質感のタイプを設定しているのは，完全鏡面反射の計算は時間的コストがかかるため，完全鏡面反射を使用しない際はその計算を行わないようにするためである (後の拡張ためでもある)．

raytrace関数の変更

完全鏡面反射を実装するにはraytrace関数の中でraytrace関数を呼び出す，つまり再帰呼び出しを使って実装することになる(リスト1)．

int raytrace(const scene_t* scene, const ray_t *eye_ray, colorf_t *out_col)
{
    /* ...省略... */
    raytrace(scene, re_ray, *col);
    /* ...省略... */
}

再帰呼び出しを用いる際は，再帰呼び出しの終了条件に注意する必要がある．
つまり迂闊に何の条件もなくリスト1のような実装を用いると条件によってはraytrace関数が無限に再帰呼び出しされる可能性がある．

再帰しているときに完全鏡面反射しない物体(MT_DEFAULT)に交差するか，別の物体と交差しなければ自然に再帰呼び出しは止まるが， 完全鏡面反射する物体が向かい合わせになっているような場合は再帰呼び出しが止まらなくなる(図4)．

これを防ぐため再帰呼び出しの回数には決め打ちの制限を設ける．
raytrace関数は以下のような構造となる(リスト2)．

/* 最大の再帰呼び出し回数 */
#define MAX_RECURSION 8

int recursive_raytrace(const scene_t* scene, const ray_t *eye_ray, colorf_t *out_col, int recursion_level)
{
   if ( recursion_level > MAX_RECURSION ) /* 再帰呼び出しの回数が制限を超えている場合 */
   {
      /* 何もしない */
      return 0;
   }
   else /* 再帰呼び出しの回数が制限以内の場合 */
   {
      /* 光線追跡の処理 */

      /* ...省略... */

      /* 完全鏡面反射を使う場合は，再帰呼び出しを行う． */
      /* その際，現在の再帰呼び出し回数(recursion_level)を増やして呼び出す． */
      recursive_raytrace(scene, re, col, recursion_level+1);

      /* ...省略... */
   }
}

int raytrace(const scene_t* scene, const ray_t *eye_ray, colorf_t *out_col)
{
    return recursive_raytrace(scene, eye_ray, out_col, 0);
}

新たにrecursive_raytrace関数を追加し，今までのraytrace関数はこの関数を単に呼び出すだけとなった．

recursive_raytrace関数は，一つを除いてraytrace関数と同じ引数を持つ．recursive_raytrace関数の最後の引数 recursion_levelは現在の再帰呼び出しの回数を表している．raytrace関数ではこの引数をゼロとしてrecursive_raytrace関数を呼び出している．

recursive_raytrace関数は，現在の再帰呼び出しの回数が最大回数(決め打ちMAX_RECURSION)を超えた場合は何もせずに終了する． それ以外の場合は，いままでのraytrace関数相当の処理を行う．

課題 [—EXCLUDE—]

課題3-2. 完全鏡面反射を実装する

完全鏡面反射の処理を実装せよ．

課題3-1. 付影処理を実装するの ソースコードをディレクトリごとコピーしてから作業を行うこと(raytracing_tk_ch8という名前でコピー)．

シーンの設定は以下のようにせよ(図5)．
scene_setting4.cとして新たにscene_setting関数を作成すること(Makefileの設定の追記も忘れないように注意する)．

図5. シーン設定

• 物体は全部で6つ
  1. 球
     • 位置：$$(-0.25, -0.5, 3)$$，半径：$$0.5$$
     • 質感は完全鏡面反射のみ
  2. 平面1(白い床)
     • 法線：$$(0,1,0)$$，位置：$$(0,-1,0)$$, 拡散反射のみ
  3. 平面2(白い天井)
     • 法線：$$(0,-1,0)$$，位置：$$(0,1,0)$$, 拡散反射のみ
  4. 平面3(右の緑の壁)
     • 法線：$$(-1,0,0)$$，位置：$$(1,0,0)$$, 拡散反射のみ
  5. 平面4(左の赤の壁)
     • 法線：$$(1,0,0)$$，位置：$$(-1,0,0)$$, 拡散反射のみ
  6. 平面5(白い奥壁)
     • 法線：$$(0,0,-1)$$，位置：$$(0,0,5)$$, 拡散反射のみ
• 光源は一つ
  1. 点光源
     • 位置：$$(0,0.9,2.5)$$，照度：$$1.0$$

生成画像は以下のようになる．

図6. 生成画像

プログラムのビルド方法および実行方法

以下のコマンドでプログラムの実行形式および画像を生成する．

以下のコマンドで生成結果を確認する．

ヒント１

ヒント２