The Textbook of RayTracing @TDU

プログラムの整理と拡張(前編)

前章までのスケッチでは様々な情報を個々のグローバル変数として保持しており，また処理をほとんど すべてdrawメソッド内に詰め込んでいたため機能拡張が困難である．

本節では，今後の拡張(反射や屈折の実装)のため，前節までのプログラムを整理する．

交差判定の整理

いままでは半直線–球の交差判定を行っていた．

半直線との交差判定の方法は，対象の形状(球，平面，円柱，立方体，etc..)ごとに異なる． しかし，どのような方法であっても交差判定の結果として交点の位置や交点における法線方向が 分かれば陰影の計算が可能である．

そこでこの交差判定の方法を抽象化してしてみよう． まず形状を表すクラスShapeを定義する．

class なんとかクラス
{
  public int hoge;
  public float piyo;

  public void doSomething() { /* ..省略.. */ }
  public char doNothing(){ /* ..省略.. */ }
}

testIntersectionメソッドは物体との交差判定を行う抽象メソッドである．引数として半直線を表すクラス Rayのインスタンスを受け取り，交点に関する情報を表すクラスIntersetionPointを返す．交点がない場合にはnullを返す． RayとIntersectionPointはそれぞれ以下のようなクラスである．

球や平面，円柱などといった具体的な形状を導入するには，Shapeクラスを継承した， それぞれの形状に対応するクラスを定義してtestIntersectionメソッドをオーバーライドすればよい．

class Hoge // 既存のクラス
{
  public int data1;
}

class Piyo extends Hoge // Hogeを継承した新しいクラス
{
  public float data2;
}

Piyo p = new Piyo(); // Piyoクラスのインスタンスを生成

// Piyoのメンバーを表示してみる
println(p.data2); // Piyoで定義された属性はもちろんのこと
println(p.data1); // 元となったHogeのメンバーも兼ね備えている!

class Hoge // 既存のクラス
{
  public void doSomething()
  {
    println("Hoge!");
  }
}

class Piyo extends Hoge // Hogeを継承した新しいクラス
{
  public void doSomething() // オーバーライド
  {
    println("Piyo!");
  }
}

Hoge h = new Hoge(); // Hogeクラスのインスタンスを生成
h.doSomething(); // "Hoge!"と表示される．

Piyo p = new Piyo(); // Piyoクラスのインスタンスを生成
p.doSomething(); // "Piyo!"と表示される．

Hoge h = new Piyo(); // Hogeクラスの変数にPiyoのインスタンスを代入．

h.doSomething(); // 何が呼び出される？

class Hoge // 既存のクラス
{
  public void doSomething()
  {
    println("Hoge!");
  }
}

class Piyo extends Hoge // Hogeを継承した新しいクラス
{
  public void doSomething() // オーバーライド
  {
    println("Piyo!");
  }
}

Hoge h = new Piyo(); // Hogeクラスの変数にPiyoのインスタンスを代入．

h.doSomething(); // 何が呼び出される？

Hoge h = new Hoge(); // Hogeクラスの変数にHogeのインスタンスを代入．

h.doSomething(); // 何が呼び出される？

1. 入力された図形データを受け取る．

2. 図形の面積を計算する．

3. 2で計算した面積をつかって何かする．

1. 入力された図形データを受け取る．

2. 図形の面積を計算する．
  if ( 三角形の場合 )
    三角形の面積を計算する．
  else if ( 四角形の場合 )
    四角形の面積を計算する．
  else if ( 円の場合 )
    円の面積を計算する．
  ...

3. 2で計算した面積をつかって何かする．

class Figure {
  public float calcArea(){ /* ..省略.. */ }
}

// 三角形クラス
class Triangle extends Figure
{
  public Point p1, p2, p3; // 頂点の座標
  public float calcArea(){ /* 三角形の面積を計算 */ }
}

// 四角形クラス
class Quadrangle extends Figure
{
  public Point p1, p2, p3, p4; // 頂点の座標
  public float calcArea(){ /* 四角形の面積を計算 */ }
}

// 円クラス
class Circle extends Figure
{
  public Point center; // 中心
  public float radius; // 半径
  public float calcArea(){ /* 円の面積を計算 */ }
}

// 1. 入力された図形データを受け取る．
Figure fig = /* 何らかの図形 */;

// 2. 図形の面積を計算する．
float area = fig.calcArea();

// 3. 2で計算した面積をつかって何かする．
println(area); // 例えば単に表示する．

class Figure {
  public float calcArea(){ /* ..省略.. */ }
}

class Figure {
  public abstract float calcArea(); // ブロック'{}'を書く必要が無い．
}

abstract class Figure {
  public abstract float calcArea(); 
}

Figure fig = new Figure(); // エラー

Figure fig = new Figure(); // これはできないが…

fig = new Triangle(); // 三角形型や…

fig = new Circle();   // 円型といった具体的な
                      // 図形クラスならインスタンスを作れる．

例えば以下のように使用する．

// 「中心位置(0,0,5)，半径1の球」のオブジェクトを生成
Shape s = new Sphere(new PVector(0,0,5), 1); 

// 「始点位置(0,0,5)，Z正方向の半直線」のオブジェクトを生成
Ray r = new Ray(new PVector(0,0,5), new PVector(0,0,1));

// 上記の球と半直線の交差判定を行う．
IntersectionPoint res = s.testIntersection(r);

if ( res != null ) // 交点あり
{
  // 表示してみる
  println(res.position); // 交点位置
  println(res.normal);   // 交点における法線方向
}

光源の整理

前回までの内容では，点光源のみを扱っていた．

光の広がり方のモデルは，点光源以外にも平行光源やスポットライトなど様々なものがある． ライティング(光の当たり方)の計算方法はそれら光源のタイプごとに異なるが，どのような タイプの光源であっても物体表面における入射ベクトルの方向と入射光の強度が分かれば 続く放射輝度(≒色)の計算が可能である．

そこで先ほどの交差判定の例と同様に，このライティングの計算を抽象化してみよう． まず，光源を表すクラスLightSourceを定義する．

lightingAtメソッドは，ライティングの計算を行う抽象メソッドである． 引数としてライティング計算を行う3次元空間中の位置(PVector)を受け取り，その位置における ライティングに関する情報を表すクラスLightingを返す．
Lightingは以下のようなクラスである．

点光源や平行光源，スポットライトといったモデルの光源を導入するには，LightSourceクラスを 継承したクラスを定義してlightingAtメソッドをオーバーライドすれば良い．

例えば以下のように使用する．

// 「位置(-5,5,5)にある白色の点光源」のオブジェクトを生成する
LightSource ls = new PointLightSource(new PVector(-5,5,5), new FColor(1,1,1));

PVector p = /* 物体との交点 */;

// 点pにおけるライティングを計算する．
Lighting ltg = ls.lightingAt(p);

// 表示してみる．
println(ltg.distance);  // 光源までの距離
println(ltg.direction); // 入射ベクトル(点pから光源に向かうベクトル)
println(ltg.intensity); // 点pにおける光源の強さ

放射輝度の計算の整理

前回までのスケッチでは三つの反射係数$$k_{a}, k_{d}, k_{s}$$を使用した．反射係数（反射率）は入射した光に対する反射する光の比率である．たとえば，当たった光の量が1.0で反射した光の量が0.7であれば反射係数は$$\frac{0.7}{1.0}=0.7$$となる．

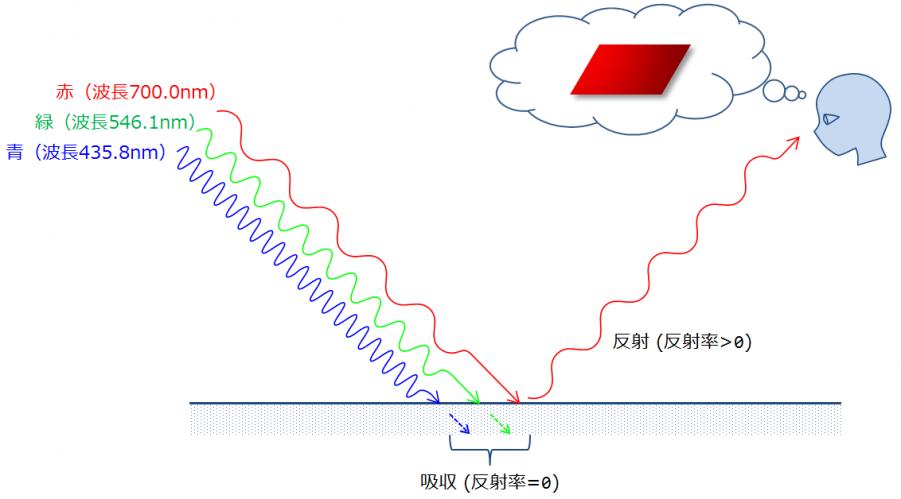
現実の物体表面では，反射係数（反射率）は光の波長によって異なる．別の言い方をすれば反射率は光の波長の関数である． たとえば（極端な例であるが）ある物体表面において，波長700nmの光の反射率が1.0で，それ以外の波長の反射率が0.0ならばその物体は赤く見える(図1)．

図1. 波長ごとに反射率は異なる

前章の実装では反射係数$$k_{a}, k_{d}, k_{s}$$が登場したが，レイトレーシング法において 物体表面の色を再現するには，これら反射係数をRGB各チャネルごとに定義する必要がある．

また，光源の強度$$I_{i}$$も環境光の強度$$I_{a}$$も単一の値として処理していた．
色の付いた光を再現するには光の強さも同様にRGB各チャネルごとに定義する必要がある．

これらは前回までのプログラムでは(穴埋めソースの通りならば)冒頭の以下の部分に相当する．

// 定数の初期化
PVector eyePos     = new PVector(0,0,-5) ; // 視点位置
PVector spherePos  = new PVector(0,0, 5) ; // 球の中心位置
float   sphereR    = 1.0                 ; // 球の半径
  
PVector lightPos   = new PVector(-5,5,-5); // 光源位置
float   lightIntensity   = 1.0           ; // 光源の強度
float   ambientIntensity = 0.1           ; // 環境光の強度
  
float   kAmb      = 0.01; // 環境光反射係数
float   kDif      = 0.69; // 拡散反射係数
float   kSpe      = 0.30; // 鏡面反射係数
float   shininess = 8   ; // 光沢度

環境光反射係数(kAmb)，拡散反射係数(kDif)，鏡面反射係数(kSpe)が「物体の反射係数」， 光源の強度(lightIntensity)，環境光の強度(ambientIntensity)が「光の強さ」である．

これらは全てfloat型であるが，カラー化にはこれをRGB3チャンネルに対して定義する必要がある．
たとえば環境光反射係数なら，単一のfloat値だったものが，Rチャンネルの環境光反射係数， Gチャンネルの環境光反射係数，Bチャンネルの環境光反射係数，といった具合に3つのfloat値にする 必要がある．「光の強さ」も同様である．

これら「3つのfloat値」を表すため以下のようなクラスFColorを導入する．

見ての通り，red，green，blueという名前のパブリックなfloat型の属性を有するクラスである．以下のように使用する．

値の設定はsetメソッドかコンストラクタを使用する．

FColor col1 = new FColor(); // 初期化

col1.set(1.0, 0.5, 0.25); // RGB各チャンネルに値を設定．以下と同じ．
// col1.red   = 1.0;
// col1.green = 0.5;
// col1.blue  = 0.25;

// コンストラクタで値の指定も可能
FColor col2 = new FColor(0.3, 0.2, 0.1); // RGB各チャネルを指定して生成
FColor col3 = new FColor(0.1); // RGB全て0.1で生成

PVectorで説明したように，FColorもクラスであるためやはり意図しない エイリアスを作ってしまわないように注意が必要である．インスタンスのコピーが必要な場合は，PVectorと同様にcopyメソッドを用いる．

FColor col4 = col2.copy(); // インスタンスをコピー(PVectorと同様)

FColorもPVectorと同様にprint/printlnメソッドで(正確には文字列と結合することで)，表示が可能である．

println(" color : " + col2); // 表示．以下のように表示される．
// color : [ 0.3, 0.2, 0.1 ]

色の同士の計算として加算代入と乗算代入をサポートしている．以下のように使用する．

col1.add(col2); // 加算代入．以下と同じ．
// col1.red   += col2.red;
// col1.green += col2.green;
// col1.blue  += col2.blue;

col1.mult(col3); // 乗算代入．以下と同じ．
// col1.red   *= col3.red;
// col1.green *= col3.green;
// col1.blue  *= col3.blue;

放射輝度の値としてFColorを使う場合，放射輝度から色(Processingのcolor型)への変換に注意する必要がある． この場合FColorの値はあくまでもレイトレーシングの結果推定された物体表面における放射輝度である．

シミュレーションによって得られる放射輝度の値はいかなる値も取り得るため， いかなる放射輝度の値が32bitカラーのいかなる値に相当するのか，は事前に決めておく必要がある．

toColorメソッドはこの変換を行うメソッドである．

color c1 = col4.toColor(); // 放射輝度[0.0, 1.0]の範囲を[0, 255]に変換

color c2 = col4.toColor(2.0); // 放射輝度[0.0, 2.0]の範囲を[0, 255]に変換

color c3 = col4.toColor(1.0, 2.0, 3.0); // RGBでマッピングの範囲を変えた変換

また，記述の簡便性のため色の総乗$$\left(\prod{}{}{c_i}\right)$$を計算する colorPiというメソッドも定義してある．このメソッドは引数をいくつでも 与えることができる．以下のように使用する．

FColor col4 = colorPi(col1, col2, col3); // 総乗
// 以下と同じ結果となる
//
// col4.red   = col1.red   * col2.red   * col3.red;
// col4.green = col1.green * col2.green * col3.green;
// col4.blue  = col1.blue  * col2.blue  * col3.blue;

まとめ

ここまでに登場したクラスをまとめる．

以下は交差判定に関連するクラス群である．

以下は光源と放射輝度計算に関するクラス群である．

以下の課題でここで導入したクラスを使って前節と同じ動作をするスケッチを作成してみよう．

課題

準備

課題2-3，2-4では，本節で導入したクラスライブラリをスケッチに追加する必要がある．以下の手順を実行せよ．

D.1) 新規にスケッチを作成する．

D.2) 空のスケッチを保存する．ファイルメニューの保存をクリックする．

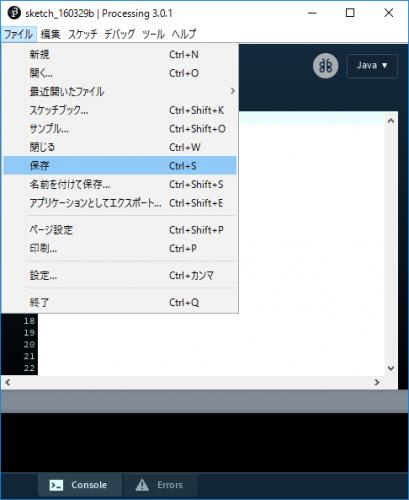
D.3) 以下のようなダイアログが表示されるので，HalfRayTracingという名前で保存する．

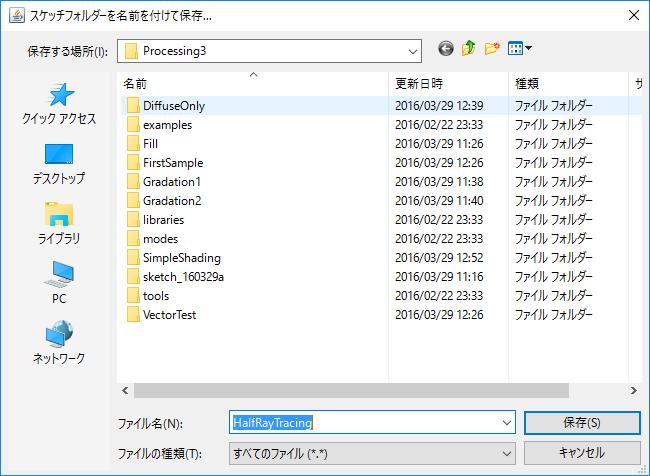
D.4) タブの隣の下向きの三角形(▼)をクリックし，新規タブを選択する．

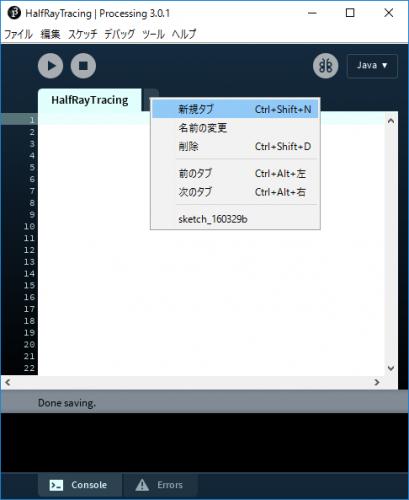
D.5) ファイル名の入力を求められるので，適当な名前を入力する．ここではGeometryUtilsと入力してOKボタンをクリックする．

D.6) 空のソースファイルがスケッチに追加される．

D.7) 以下のボタンをクリックするとクリップボードに必要なソースコードがコピーされるので，D.6の空のソースファイルにペーストする．

ここをクリックして
ソースコードをコピー

D.8) この状態で一度保存する．

課題2-3. testIntersectionメソッドを実装する

前節でコピー＆ペーストしたソースコードでは，SphereクラスのtestIntersectionメソッドが 未実装の状態となっている．このメソッドを実装せよ．

以下の手順に従え．

E.1) 以下のボタンをクリックするとtestIntersectionメソッドのテストドライバ(≒テストコード)がクリップボードにコピーされるので， これをスケッチHalfRayTracingのメインのタブにペーストする．

ここをクリックして
テストドライバをコピー

テストドライバには一切手を加えてはならない.

E.2) SphereクラスのtestIntersectionメソッドは，GeometryUtilsの113行目付近にある．元から書いてある2行を削除してこのメソッドを実装する．

testIntersectionメソッドの仕様は「交差判定の整理」の通りであるが，一応再掲する．

testIntersectionメソッドは物体との交差判定を行う抽象メソッドである．引数として半直線を表すクラス Rayのインスタンスを受け取り，交点に関する情報を表すクラスIntersetionPointを返す．交点がない場合にはnullを返す．

E.3) SphereクラスのtestIntersectionメソッドを実装できたら，を押して実行する．

SphereクラスのtestIntersectionメソッドを正しく実装できた場合，コンソールに以下のように表示されるはずである．

ヒント

課題2-4. 「最初の陰影処理」の再実装

本節で導入したクラスライブラリを使用して，「課題2-2. 最初の陰影処理（環境光，拡散反射光，鏡面反射光）」を実装せよ．
課題2-3のメインのタブにコピー&ペーストしたテストドライバを全て削除し，改めて実装を始めること．

シーン設定などは「課題2-2」に準じるが， ライティングに関わるパラメータを以下のように変更する．

• 環境光反射係数
  • $$k_{a}=(0.01, 0.01, 0.01)$$
• 拡散反射係数
  • $$k_{d}=(0.69, 0.00, 0.00)$$
• 鏡面反射係数
  • $$k_{s}=(0.30, 0.30, 0.30)$$
• 光沢度
  • $$\alpha=8$$
• 環境光の強度
  • $$I_{a}=(0.10, 0.10, 0.10)$$
• 直接光の強度
  • $$I_{i}=(1.00, 1.00, 1.00)$$

括弧$$()$$で囲まれた3つの実数の組は，それぞれRチャンネル，Gチャンネル，Bチャンネルの反射係数/光の強度を意味する． 拡散反射係数のみG,Bチャンネルの反射係数がゼロとなっている．したがって，シーン中の球は赤く見えるはずである．生成結果は下図のようになる．

図2. HalfRayTracingの生成画像

ヒント

課題2-5. 複数の物体を表示する

「課題2-4. 『最初の陰影処理』の再実装」を改造して，複数の物体を表示できるように変更せよ．
課題2-4のスケッチをHalfRayTracing_MultiShapesという名前で別名保存(ファイルメニューの名前を付けて保存をクリックして保存)してからとりくむこと．

表示すべき物体は以下である．

1. 球1
   • 中心$$(3,0,25)$$，半径$$1$$
2. 球2
   • 中心$$(2,0,20)$$，半径$$1$$
3. 球3
   • 中心$$(1,0,15)$$，半径$$1$$
4. 球4
   • 中心$$(0,0,10)$$，半径$$1$$
5. 球5
   • 中心$$(-1,0,5)$$，半径$$1$$
6. 平面
   • 法線方向$$(0,1,0)$$, 位置$$(0,-1,0)$$

後述の物体のリストには，物体のデータをこの順序で格納すること．勝手に順序を変更してはならない．

// 「法線方向が(1,1,1)で，原点(0,0,0)を通る平面」のオブジェクトを生成
Plane pln = new Plane(new PVector(1,1,1), new PVector(0,0,0));

// 表示してみる
println(pln.normal);   // 法線方向
println(pln.position); // この平面が通る点

Plane pln = /* 何らかの平面 */;
Ray ray = /* 何らかの半直線 */;

IntersectionPoint intP = pln.testIntersection(ray);
if( intP != null ) // 交差あり
  // ..何か処理..
else // 交差なし
  // ..何か処理..

複数の物体，つまり複数のShapeクラスのインスタンス(つまり物体のリスト)を保持する方法はいくつかあるが，ここではArrayList<E>を用いる． 以下のように使用する．

ArrayList<Shape> shapes; // 物体のリスト
// ..中略..

void setup()
{
  // ..中略..
  shapes = new ArrayList<Shape>(); // 物体のリストを生成

  Sphere sph1 = /* 何らかの球オブジェクト */ ;
  shapes.add(sph1); // 物体のリストに追加

  Sphere sph2 = /* 何らかの球オブジェクト */ ;
  shapes.add(sph2); // 物体のリストに追加

  Plane pln1 = /* 何らかの平面オブジェクト */ ;
  shapes.add(pln1); // 物体のリストに追加
}

(※ SphereやPlaneはそれぞれ球や平面を表すクラスである．これらはShapeクラスのサブクラスであるため，Shapeクラスと代入互換性を持つ．そのためShapeのリストに追加することができる．)

リスト内の要素を反復するには以下のようにする．

// リスト内の各要素を処理する
for(int i = 0; i < shapes.size(); ++i)
{
  Shape shp = shapes.get(i);
  // 何かの処理
}//for

// 以下でも同じ(こちらの方が簡潔)
for(Shape shp : shapes)
{
  // 何かの処理
}//for

生成結果は下図のようになる．

図2. HalfRayTracing_MultiShapesの生成画像

ヒント1

+ クリックで表示 クリックで非表示

shapesに入っている全ての物体を反復して，視線レイと交点を持つ物体を探す． 視線レイと交点を持つ物体の中で，放射輝度を計算するのは視点に最も近い物体である．

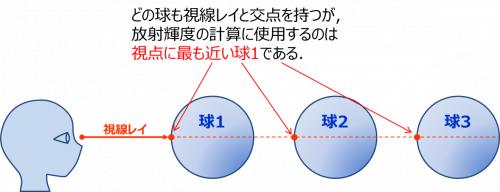
誤ってshapesのうち視線レイと交点を持つ最初の物体を放射輝度の計算に使ってしまわないように注意せよ． shapesに物体が視線に近い順で格納されているとは限らない．

-クリックで非表示

ヒント2