[—ATOC—] 1 [—AUTO_SECTION_NUMBER—] 1
影を付ける
陰と影
陰と影は異なる概念である.
日本語だと音が同じであるため紛らわしいが両者は異なる(図1).
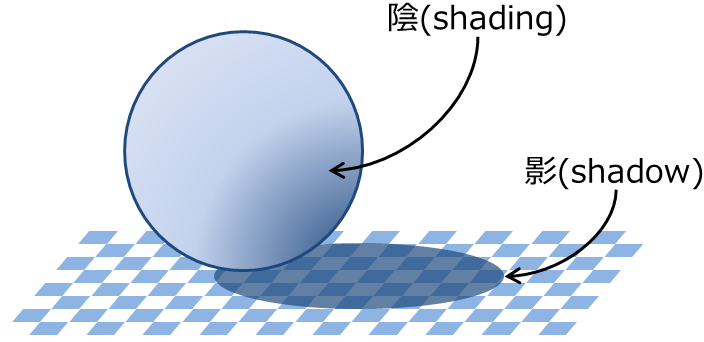
図1. 陰(shading)と影(shadow)
陰(shading)は物体表面の形状によって,その物体自身に出来る濃淡である.
Chapter5. 陰を付けるで議論している影である.
影(shadow)は物体の輪郭が別の物体に投影されたものである.
本章ではこちらの影を扱う.
影の重要性
課題2-4. 床を付ける(scene_setting関数)の 生成画像を再掲する(図2).

図2. 課題2-4の生成画像
この課題のシーン設定は以下のようになっている(図3).
- 球
- 中心:$$(0,0,5)$$
- 半径:$$1.0$$
- 平面
- 法線:$$(0,1,0)$$
- 位置:$$(0,-1,0)$$
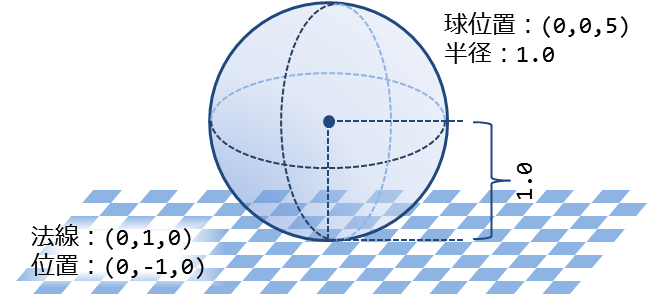
図3. 課題2-4のシーン設定
実は球と床(平面)は接触している.
しかし図2を見ただけでは球と平面が接していることを汲み取ることは難しい.これは球によって作られるはずの影が存在しないためである. 影はシーンにおける物体の位置を読み取る重要な要素である.
付影処理
付影処理は比較的容易に実装できる.
視線と物体の交点が見つかり個々の光源からの反射光を計算するとき,に光源と交点の間に遮る物体が存在するか否かを調べればよい(図4).
視線とシーン内のすべての物体との交差判定を行うときと同じように,入射ベクトル方向のレイと物体が存在するかを調べる.レイの始点は視線と物体の交点である.このレイをシャドウレイと呼ぶことがある.
交差判定を行う際,物体までの距離に注意する.シャドウレイの方向に物体が見つかっても,光源よりも遠い位置にあるならば光を遮っているとは言えない.そのため視線と物体の交点と光源の間の距離と, シャドウレイと交差した物体までの距離を常に比較する必要がある.
点光源の場合
点光源の場合は,視線との交点と光源との距離$$D_{\ell}$$は容易に計算できる.
視線との交点の位置が$$\vec{\bf p_{\cal i}}$$, 点光源の位置が$$\vec{\bf p_{\ell}}$$ならば, その間の距離は$$D_{\ell}=|\vec{\bf p_{\ell}}-\vec{\bf p_{\cal i}}|$$となる.
これは正規化する前の入射ベクトル$$\vec{\bf \ell}$$の大きさ等しい.
平行光源の場合
平行光源の場合は,視線との交点と光源との距離$$D_{\ell}$$は特殊な扱いとなる.
平行光源は,光源の位置という概念はなく方向しかない.そのため平行光源は光源位置が無限遠方($$D_{\ell}=\infty$$)にあると考える.
付影処理の実装
get_nearest_shape関数
付影処理を実装するためには,シャドウレイとシーン内の物体の物体との交差判定を行う必要がある.
このためには視線レイとシーン内の物体との交差判定を行うのと同様にget_nearest_shape関数を用いる.
get_nearest_shape関数は,与えられたレイとシーン内の全ての物体との交差判定を行い最もレイの始点に近い物体を探す関数である.
シャドウレイの方向に一つでも交点が見つかれば,視線と物体の交点と光源の間に遮蔽物があると判定できる. したがって,条件に合致する物体が見つかれば,判定処理を切り上げても良い.
get_nearest_shape関数にはこのための引数exit_once_foundが存在する.
この引数に非ゼロ値を渡すと,条件に合致する物体が見つかった場合に直ちにreturnする.
シャドウレイ
シャドウレイの始点に注意する必要がある.
前節で「シャドウレイの始点は視線と物体の交点」と述べたが,これをそのまま実装してしまうとうまくいかない.そのようなシャドウレイは必ずその物体自身と交差する.
なぜなら,視線と物体の交点は,物体上の点であるため,その点をレイの始点としてしまうと交差判定の際にその物体自身が最も近い物体として判定されてしまう.
これを避けるため,シャドウレイの始点を入射ベクトル側にほんの少しずらす必要がある(図5).

図5. シャドウレイの始点を入射ベクトル側にほんの少しずらす
(自分自身と交差した場合は交差と見なさないように実装する方法もある.)
従ってシャドウレイおよび光源までの距離を以下のように変更する必要がある.
- シャドウレイ
- 始点:$$\vec{\bf p_{\cal i}}+\epsilon\vec{\ell}$$
- 方向:$$\vec{\ell}$$
- $$\vec{\bf p_{\cal i}}$$:交点の位置ベクトル
- $$\vec{\ell}$$:入射ベクトル(光源に向かう方向ベクトルであることに注意)
- $$\epsilon$$:微小距離
- 光源までの距離
- $$D’_{\ell }=D_{\ell}-\epsilon$$
$$\epsilon$$は微小距離であり,$$\frac{1}{32}$$,$$\frac{1}{128}$$, $$\frac{1}{512}$$などを使う.
$$\epsilon$$は定数であるため,翻訳単位のどこか(たとえばraytrace関数の直前など)で以下のようなマクロを作ると良いだろう.
#define EPSILON (1.0f/512)
課題 [—EXCLUDE—]
課題3-1. 付影処理を実装する
raytrace関数を変更し付影処理を実装せよ.
課題2-5. ランダムに球を100個配置するの ソースコードをディレクトリごとコピーしてから作業を行うこと(raytracing_tk_ch7という名前でコピー).
シーン設定は課題2-4. 床を付ける(scene_setting関数)に準じる(球が一つと床のみ).
生成画像は図6のようになる.

図6. 生成画像
プログラムのビルド方法および実行方法
以下のコマンドでプログラムの実行形式および画像を生成する.
以下のコマンドで生成結果を確認する.
ヒント1
raytrace関数で,各光源について処理する部分に追加する.
入射ベクトル$$\vec{\bf \ell}$$が確定した段階で,
- 視線と光源の距離$$D_{\ell}$$を計算する.
- 点光源の場合は$$D_{\ell}=\left|\vec{\bf p_{\ell}} – \vec{\bf p_{\cal i}}\right|-\epsilon$$である.
- 平行光源の場合は$$D_{\ell}=\infty$$である.
- シャドウレイを作る.
- 始点:$$\vec{\bf p_{\cal i}}+\epsilon\vec{\bf \ell}$$
- 方向:$$\vec{\bf \ell}$$
- ここでは$$\epsilon=\frac{1}{512}$$を用いる
- シャドウレイとシーン内の全ての物体との交差判定を行う.
- 交差があった場合
- その光源による反射光を計算を省略する.
- 交差がなかった場合
- 通常通り反射光の計算を行う.
- 交差があった場合
ヒント2
ソース穴埋め
必要なコードは短いのでナシ

0 Comments.