[—ATOC—] 1 [—AUTO_SECTION_NUMBER—] 1
課題1-7補足問題
ここの問題は課題1-7 レイと球の交差判定
が難しいと感じたら取り組んでください.
十分にヒントを得られたと思ったら,途中でやめて課題1-7 レイと球の交差判定に戻っても構いません.
シーン設定
課題1-7 レイと球の交差判定で想定しているシーンを再掲する.
- 視点位置
- $$\vec{\bf p_{\cal e}}=(0,0,-5)$$
- スクリーン位置
- 左上$$(-1,1,0)$$, 右上$$(1,1,0)$$, 右下$$(1,-1,0)$$, 左下$$(-1,-1,0)$$
- 球
- 中心位置$$\vec{\bf p_{\cal c}}=(0,0,5)$$
- 半径$$radius=1.0$$
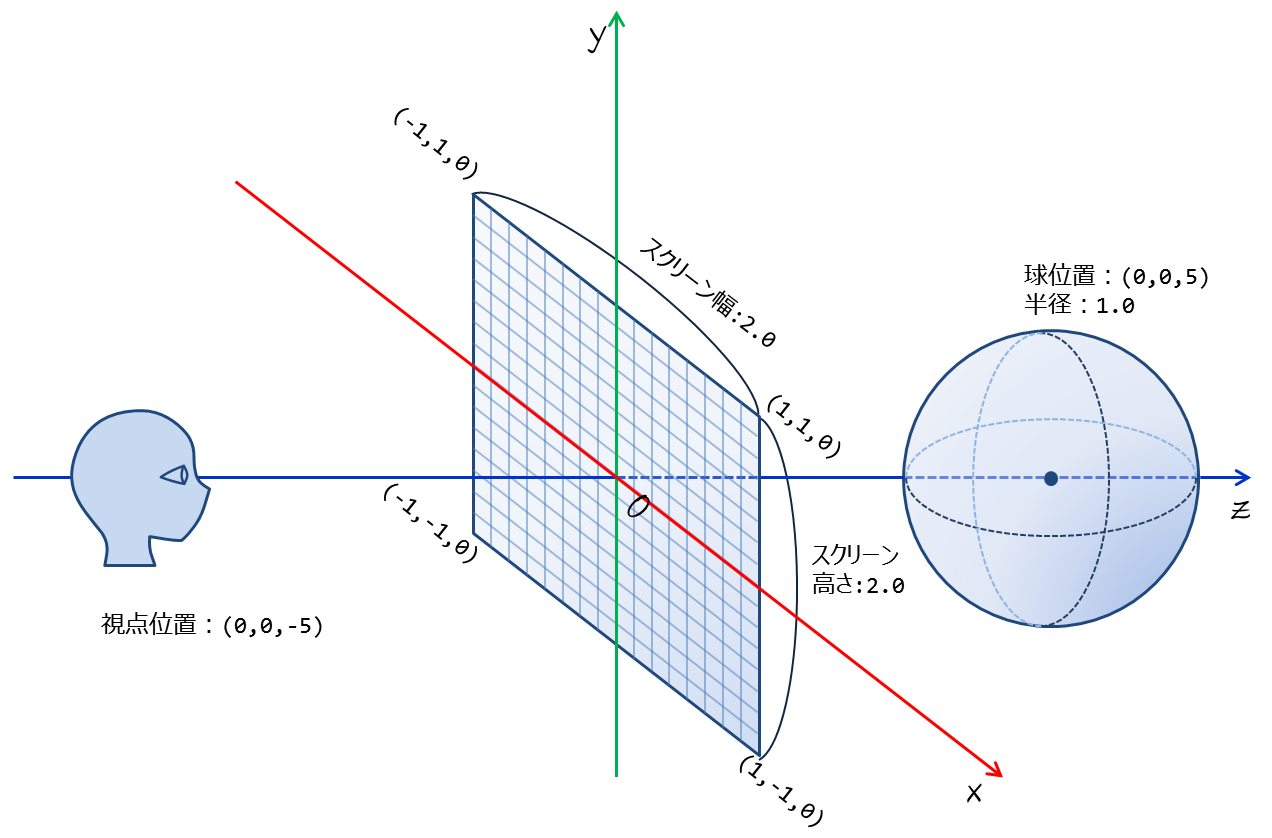
図1. シーン設定
補足問題1
スクリーン座標$$(382,255)$$を,三次元空間上の座標に変換するプログラムを作成せよ.
変換方法は4-1.2. スクリーン座標の変換の通りである. 変換式を以下に再掲する.
#include <stdio.h>
#include "vector_utils.h"
#define WIDTH 512
#define HEIGHT 512
int main()
{
int x_s = 382;
int y_s = 255;
vector_t pw;
pw.x = /* *** 穴埋め *** */;
pw.y = /* *** 穴埋め *** */;
pw.z = /* *** 穴埋め *** */;
printf("(%d,%d) -> %s\n", x_s, y_s, vector_str(&pw));
return 0;
}
結果は以下のようになるはずである.
プログラムのビルド方法および実行方法
以下のコマンドでプログラムの実行形式を生成する.
問題なくビルドできたら,以下のコマンドで実行する.
補足問題2
2014-04-25: 穴埋めコードの穴埋め位置に番号を振った.ヒント1~5を追加.
視点$$\vec{\bf p_{\cal e}}$$から,スクリーン上の点$$\vec{\bf p_{\cal w}}=(-0.4, 0, 0)$$への半直線は 球と交点を持つかどうかプログラムを使って調べよ.交差する場合は「Yes!」,しない場合は「No…」と表示すること.
ソースファイル名はone_sample.cとする.
#include <stdio.h>
#include "vector_utils.h"
int main()
{
vector_t eye_pos = { 0, 0, -5 };/* 視点位置 */
vector_t sphere_pos = { 0, 0, 5 }; /* 球の中心 */
float sphere_r = 1; /* 球の半径 */
vector_t pw = { -0.4, 0, 0 };/* スクリーン上の点 */
vector_t eye_dir; /* 視線方向ベクトル */
vector_t s_c; /* 視点 - 球の中心 */
float A,B,C,D; /* 二次方程式Ax^2+Bx+C=0および判別式D */
/* ****************************** */
/* */
/* */
/* 穴埋め1 */
/* */
/* */
/* ****************************** */
A = /* *** 穴埋め2 *** */;
B = /* *** 穴埋め3 *** */;
C = /* *** 穴埋め4 *** */;
D = /* *** 穴埋め5 *** */;
if ( /* 穴埋め6 */ )
{
printf("Yes!\n");
}
else
{
printf("No...\n");
}
return 0;
}
結果は交差するはずである(視点と球の位置関係を思い浮かべてみよう).
プログラムのビルド方法および実行方法
以下のコマンドでプログラムの実行形式を生成する.
問題なくビルドできたら,以下のコマンドで実行する.
ヒント1
キーボードから手を離せ.話はそれからだ.
- 「理屈」を理解することなしにコードは書けない.「交点の有無を調べる方法」を理解しているかどうか自分に問いただしてみよ.
- それを自分の言葉で説明できないうちは,まだ「理屈」を理解していない.
- 「理屈」の理解をなしにして,テキストエディタを開きキーボードに手を置いたところで全くの無駄である.まずは「理屈」の理解に努めよ.
理屈
- tの方程式,$$At^2+Bt+C=0$$の係数$$A$$,$$B$$,$$C$$がわかれば,交差の有無を調べることができる.
- その方法は,判別式$$D=B^2-4AC$$の値が正の数かゼロか負の数かを調べることである.
以下を試みよ.
- まず,プログラミングとは関係なしに,ノートと手計算を駆使して交差の有無を調べよ.
ヒント2
以下のことを検討せよ.
- 係数$$A$$,$$B$$,$$C$$を計算するために必要なベクトルをすべて洗い出せ.
- 必要なベクトルを全てノートに書き出せ.必要ならば適切な名前や記号を付けよ.
- 洗い出したベクトルそれぞれについて以下のことを調べよ.
- 【Q1】そのベクトルを格納するために必要な変数が,穴埋めコードの中にあるかどうか?(ある/ない)
- 【Q2】その変数にはすでに必要な値が代入されているか?(いる/いない)
- 【Q3】必要な値が代入されていない場合,それを代入することは可能か.以下の項目を調べよ.
- 【Q3-1】その値を計算するための数式を書き出せ(C言語のコードではなく,数式で).
- 【Q3-2】その数式の値を計算するのに必要な値はそろっているか?(そろっている/そろっていない)
- 【Q3-3】計算に必要な値は,穴埋めコードの中のどこに当たるか.
- 【Q3-4】Q3-1で検討した数式を,C言語で書き表すことはできるか?
ヒント3
穴埋めの位置ですべきこと
- 穴埋め1
- $$\vec{\bf d_{\cal e}}$$を計算する.
- $$\vec{\bf m}$$を計算する.
- 穴埋め2
- 係数Aの値を計算する.
- 穴埋め3
- 係数Bの値を計算する.
- 穴埋め4
- 係数Cの値を計算する.
- 穴埋め5
- 判別式Dの値を計算する.
- 穴埋め6
- 判別式Dの値から,交点を持つ条件を書く.
凡例
- $$\vec{\bf c}$$
- 球の中心点$${\cal c}$$の位置ベクトル
- $$r$$
- 球の半径
- $$\vec{\bf p_{\cal e}}$$
- 視点の位置ベクトル
- $$\vec{\bf p_{\cal w}}$$
- スクリーン上の点$${\cal p_{w}}$$の位置ベクトル
- $$\vec{\bf d_{\cal e}}$$
- 視線ベクトル
- $$\vec{\bf m}$$
- $$\vec{\bf p_{\cal e}}$$から$$\vec{\bf c}$$を引いたベクトル
ヒント4
$$\leftarrow$$は代入を表す.
- 穴埋め1
- $$\vec{\bf d_{\cal e}}\leftarrow\vec{\bf p_{\cal w}}-\vec{\bf p_{\cal e}}$$
- $$\vec{\bf m}\leftarrow\vec{\bf p_{\cal e}}-\vec{\bf c}$$
- 穴埋め2
- $$A\leftarrow\left|\vec{\bf d_{\cal e}}\right|^{2}$$
- あるいは$$A\leftarrow\vec{\bf d_{\cal e}}\cdot\vec{\bf d_{\cal e}}$$
- $$A\leftarrow\left|\vec{\bf d_{\cal e}}\right|^{2}$$
- 穴埋め3
- $$B\leftarrow2\left(\vec{\bf d_{\cal e}}\cdot\vec{\bf m}\right)$$
- 穴埋め4
- $$C\leftarrow\left|\vec{\bf m}\right|^{2}-r^{2}$$
- あるいは$$C\leftarrow\left(\vec{\bf m}\cdot\vec{\bf m}\right)-r^{2}$$
- $$C\leftarrow\left|\vec{\bf m}\right|^{2}-r^{2}$$
- 穴埋め5
- $$D\leftarrow B^2-4AC$$
- 穴埋め6
- $$D\geq0$$
ヒント5
- $$\vec{\bf c}$$
- 変数sphere_pos(vector_t型)
- $$r$$
- 変数sphere_r(float型)
- $$\vec{\bf p_{\cal e}}$$
- 変数eye_pos(vector_t型)
- $$\vec{\bf p_{\cal w}}$$
- 変数p_w(vector_t型)
- $$\vec{\bf d_{\cal e}}$$
- 変数eye_dir(vector_t型)
- $$\vec{\bf m}$$
- 変数s_c(vector_t型)
補足問題3
2014-04-20: スクリーン座標を修正
スクリーン座標$$(382,255)$$を三次元空間上の座標$$\vec{\bf p_{\cal w}}$$に変換し,さらに視点から$$\vec{\bf p_{\cal w}}$$への 半直線が球と交差するかどうか調べるプログラムを作成せよ.交差する場合は「Yes!」,しない場合は「No…」と表示すること.
ソースファイル名はone_conv_sample.cとする.
(穴埋めソースは掲載しない.補足問題1および2を応用すれば作ることができる.)
結果は交差するはずである.
プログラムのビルド方法および実行方法
以下のコマンドでプログラムの実行形式を生成する.
問題なくビルドできたら,以下のコマンドで実行する.
補足問題4
スクリーン座標$$x,y$$を,三次元空間上の座標に変換するプログラムを作成せよ. スクリーン幅は512,高さは512である.
ソースファイル名はall_conv.cとする.
(穴埋めソースは掲載しない.補足問題1および課題1-1 最初のプログラムを応用すれば作ることができる.)
結果は以下のようになる(出力結果全体は非常に長大になるため割愛している.).
プログラムのビルド方法および実行方法
以下のコマンドでプログラムの実行形式を生成する.
問題なくビルドできたら,以下のコマンドで実行する.
補足問題5
スクリーン座標$$x,y$$を,三次元空間上の座標に変換し,変換後の各点を通る
半直線が球と交点を持つかどうかを調べるプログラムを作成せよ.
コンソールにはスクリーン座標と,「Yes!」(交差する場合)あるいは「No…」(交際しない場合)を表示すること.
ソースファイル名はall_sample.cとする.
出力結果は非常に長大なため以下のようにして結果の一部だけを表示させて確認すること.
プログラムのビルド方法および実行方法
以下のコマンドでプログラムの実行形式を生成する.
問題なくビルドできたら,以下のコマンドで実行する.
0 Comments.