最初の実装
ここまでで,
- Processingによる基本的な画像処理
- レイと幾何物体の交差判定
を説明した.本章ではいよいよレイトレーシング法の実装を始める.
処理手順
基本的な処理手順に関しては1-1.1. アルゴリズムを参照せよ.
最初の実装では簡単のため陰影付けを行わない.また,物体はただ一つの球に限定する.
そしてレイが球と交点を持つならば赤,交点を持たないならば青を出力することとする.
したがって,処理手順は以下のように簡略化される.
1. 視点の位置を決める.
2.
for(yを0からH-1まで繰り返す)
{
for(xを0からW-1まで繰り返す)
{
3. 視点位置から点(x,y)に向かう半直線と球との交差判定を行う.
4.
if(球と交差する場合)
(x,y)の画素に赤を出力する.
else
(x,y)の画素に青を出力する.
}
}
Wは画像の幅,Hは画像の高さである.
スクリーン座標の変換
最終的な出力を得るにはX座標0から画像幅-1,Y座標0から画像高さ-1のすべての座標について処理をして,画像の全ての画素を埋める必要がある.
for(int y = 0; y < height; ++y)
{
for(int x = 0; x < width; ++x)
{
/* 画素ごとの処理 */
}
}
簡易化した処理手順を再掲する.
1. 視点の位置を決める.
2.
for(yを0からH-1まで繰り返す)
{
for(xを0からW-1まで繰り返す)
{
3. 視点位置から点(x,y)に向かう半直線と球との交差判定を行う.
4.
if(球と交差する場合)
(x,y)の画素に赤を出力する.
else
(x,y)の画素に青を出力する.
}
}
強調した部分に着目する.
視点位置は三次元空間上の座標である.
点(x,y)は,画像中の座標である.
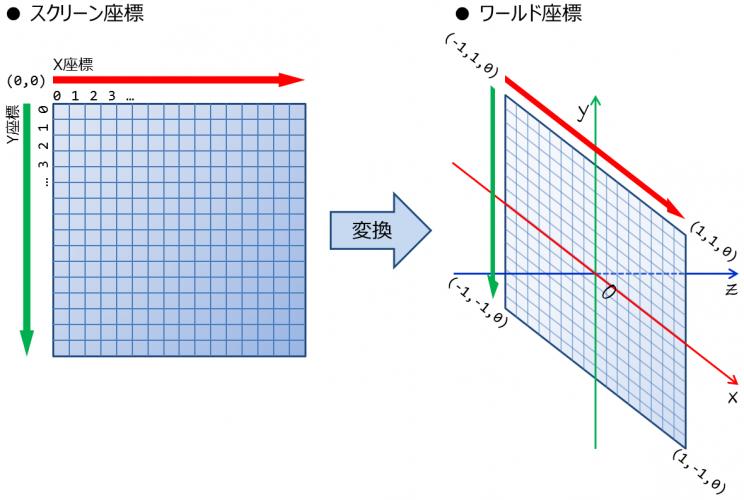
実際に画像のすべての画素を埋めていく際に扱う座標は,画像の左上を(0,0)とするスクリーン座標なので, これを三次元空間上の座標にするためには変換を行う必要がある.
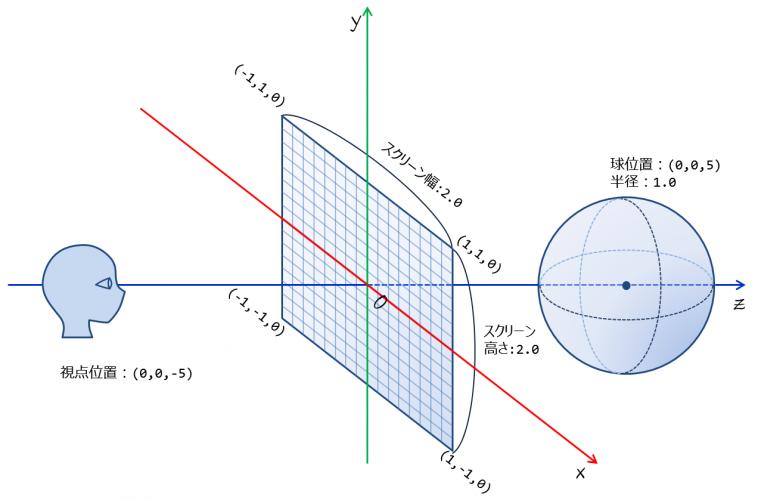
今回は三次元空間上のスクリーンを,原点を中心とした幅2.0,高さ2.0の矩形(X-Y平面)とする(図1).
スクリーン座標$$(x_{s},y_{s})$$から三次元座標$$(x_{w},y_{w},z_{w})$$への変換は各々以下のようになる.
$$W,H$$は,それぞれ画像の幅と高さである.
このテキストではこのセクションのように端々に補足説明が入っている. これらのセクションは必ずしも読む必要はない.
読んでも結論は同じであるため,本当に興味があり理解できる自信のあるものだけが読むこと.
スクリーンの位置と大きさを図1のように定めたので,四隅のスクリーン座標と三次元座標は以下のように対応する.
| 位置 | スクリーン座標(x,y) | 三次元座標(x,y,z) | |
|---|---|---|---|
| 左上 | ( 0, 0) | → | (-1, 1,0) |
| 右上 | (W-1, 0) | → | ( 1, 1,0) |
| 右下 | (W-1,H-1) | → | ( 1,-1,0) |
| 左下 | ( 0,H-1) | → | (-1,-1,0) |
※ W,Hは画像の幅と高さ.
※ 座標は0から始まるので,最大値がW-1やH-1になることに注意せよ.例えば幅32ピクセル,高さ32ピクセルの画像であれば,x座標は0~31,y座標は0~31までとなる.
もちろんスクリーンの位置と大きさは他にいくらでもとりようがある.後述するが,このテキストでは視点位置を$$(0,0,-5)$$の位置にとっていて, スクリーンまでの距離が$$5$$,スクリーンの幅(と高さ)$$2$$で,対角画角がおおよそ32度となるようなカメラを想定している(35mm判換算で焦点距離75mmの中望遠レンズ相当). 画角をより広くもとることも狭くもとることも可能だが数値がややこしくなる.
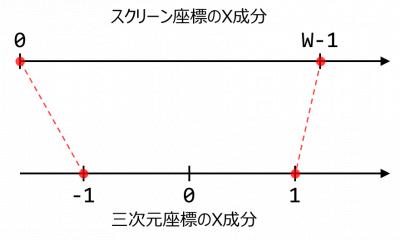
さて,上表の関係から変換式を作る必要があるがこれは難しい話ではない.まず表のX座標に着目してみよう.
| 位置 | スクリーン座標(x,y) | 三次元座標(x,y,z) | |
|---|---|---|---|
| 左上 | ( 0, 0) | → | (-1, 1,0) |
| 右上 | (W-1, 0) | → | ( 1, 1,0) |
| 右下 | (W-1,H-1) | → | ( 1,-1,0) |
| 左下 | ( 0,H-1) | → | (-1,-1,0) |
スクリーン座標のX成分が0のとき,三次元座標のX成分は-1となり,W-1のときは1となっている(図2).
このような値の範囲の変換をする場合には,対象の区間を実数の$$[0,1]$$の範囲に変換すると簡単である.
そのためにはスクリーン座標のX成分を,最大値であるW-1で割ればよい.
左辺の被除数がX成分,右辺の値が範囲変換後の値である.$$[0,W)$$の範囲が,$$[0,1]$$に変換されている. 三次元座標のX成分は$$[-1,1]$$の区間である.区間の大きさは$$2.0$$である.$$[0,1]$$の区間の大きさは$$1.0$$であるため区間の大きさを合わせるために2倍する.
このままだと,変換したスクリーン座標のX成分は単に$$[0,2]$$の区間となる.三次元座標のX成分は$$[-1,1]$$の区間であるため,これらを合わせるため, $$[0,2]$$から1を引く.
これでスクリーン座標の値の区間$$[0,W)$$を,目的である三次元座標の区間$$[-1,1]$$に変換することができた. まとめると,スクリーン座標のX成分$$x_s$$と三次元座標のX成分$$x_w$$は以下の関係にある.
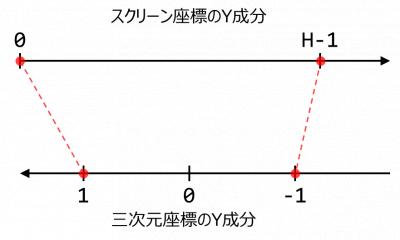
同様にY成分にも着目してみよう.
| 位置 | スクリーン座標(x,y) | 三次元座標(x,y,z) | |
|---|---|---|---|
| 左上 | ( 0, 0) | → | (-1, 1,0) |
| 右上 | (W-1, 0) | → | ( 1, 1,0) |
| 右下 | (W-1,H-1) | → | ( 1,-1,0) |
| 左下 | ( 0,H-1) | → | (-1,-1,0) |
スクリーン座標のY成分が0のとき,三次元座標のY成分は1となり,H-1のときは-1となっている(図3).
X成分の場合と似ているが区間の向きが逆転している.
では先ほどと同じようにスクリーン座標のY成分の区間を$$[0,H)$$から$$[0,1]$$に変換しよう.つまりスクリーン座標のY成分を$$H-1$$で割る.
三次元座標のY成分は$$[-1,1]$$の区間である.区間の大きさは$$2.0$$である.$$[0,1]$$の区間の大きさは$$1.0$$であるため区間の大きさを合わせるために2倍する.
このままだと,変換したスクリーン座標のY成分は単に$$[0,2]$$の区間となる.三次元座標のY成分は$$[-1,1]$$の区間であるため,これらを合わせるため, $$[0,2]$$から1を引く.
ここまではX成分と同じだが,スクリーン座標のY成分が0のとき,三次元座標のY成分は1となり,H-1のときは-1となっていたことを思いだそう.
上の式ではスクリーン座標のY成分が0とき三次元座標のY成分(右辺)が-1であり,H-1のときは1であり本来の対応関係とは符号が反転している.
これを合わせるため,スクリーン座標のY成分に-1を掛ける.
これでY成分も目的の区間に変換することができた.
まとめると,スクリーン座標のY成分$$y_s$$と三次元座標のX成分$$y_w$$は以下の関係にある.
最後にZ成分に着目する.
| 位置 | スクリーン座標(x,y) | 三次元座標(x,y,z) | |
|---|---|---|---|
| 左上 | ( 0, 0) | → | (-1, 1,0) |
| 右上 | (W-1, 0) | → | ( 1, 1,0) |
| 右下 | (W-1,H-1) | → | ( 1,-1,0) |
| 左下 | ( 0,H-1) | → | (-1,-1,0) |
Z成分はスクリーン座標の値に依らず常にゼロである. したがって,三次元座標のZ成分$$z_w$$は,
となる.これら全てをまとめると,
となる.
実装上は上式をそのまま使ってもよいし,mapメソッドを使うこともできる.
X成分に関しては$$[0,W)$$から$$[-1,1]$$への変換,Y成分に関しては$$[0,H)$$から$$[1,-1]$$への変換なので,
int xs, ys; // スクリーン座標 float xw = map(xs, 0, width-1, -1, 1); // 2.0 * xs / (width-1) -1 と同じ float yw = map(ys, 0, height-1, 1, -1); // -2.0 * ys / (height-1) + 1 と同じ float zw = 0;
というように書くことができる.
プログラミング,とくにループの関わる部分では値がいかなる範囲で変化するのか,が重要な場合が多い.このテキストでは値の範囲を以下のように表記する.
- 閉区間
- $$[a,b]$$と表記する.$$a \le x \le b$$と同義.
- 開区間
- $$(a,b)$$と表記する.$$a \lt x \lt b$$と同義(座標の表記と紛らわしいのでこのテキストではあまり用いない).
- 半開区間
- $$[a,b)$$もしくは$$(a,b]$$と表記する.前者は$$a \le x \lt b$$,後者は$$a \lt x \le b$$と同義.
例えば以下のような典型的なforループの場合,
for(int i = 0; i < 10; ++i)
{
// 何か処理をする
}
カウンタ変数iは,0,1,2,3,4,5,6,7,8,9の順で変化する(この書き方ではループの継続条件がi < 10(iが10未満である間)なので10まで変化しない).
このiの値の区間を$$[0,10)$$と表記する($$0 \le i \lt 10$$).iは整数であるため$$[0,9]$$でも同じである($$0 \le i \le 9$$).
一般に,N回繰り返すループではカウンタ変数の値の範囲は$$[0,N)$$となる.$$[0,N-1]$$も同じ範囲を意味する.
上式により,スクリーン上の点の三次元空間中における位置を計算することができる. ここでもう一度,レイトレーシングのアルゴリズムを掲載する.
1. 視点の位置を決める.
2.
for(yを0からH-1まで繰り返す)
{
for(xを0からW-1まで繰り返す)
{
3. 視点位置から点(x,y)に向かう半直線と球との交差判定を行う.
4.
if(球と交差する場合)
(x,y)の画素に赤を出力する.
else
(x,y)の画素に青を出力する.
}
}
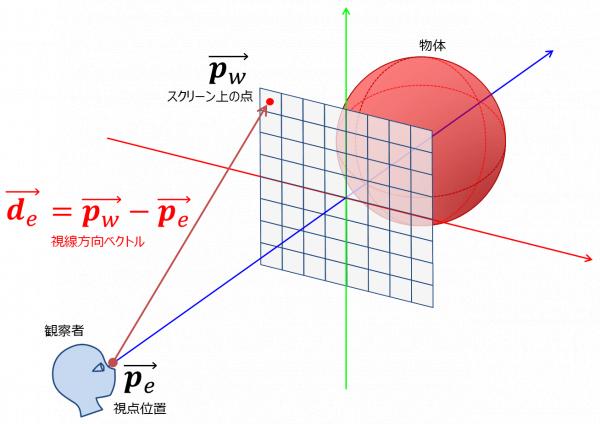
「3. 視点位置から点(x,y)に向かう半直線と球との交差判定を行う.」とある. レイ(半直線)の方程式で述べたように半直線を定義するには,始点の位置ベクトル$$\vec{\bf s}$$と方向ベクトル$$\vec{\bf d}$$が必要である. この「視点位置から点(x,y)に向かう半直線」の視点と方向ベクトルはどのように計算すればいいだろうか.
この半直線の始点は当然のことながら視点位置である.ここでは視点位置を$$\overrightarrow{\bf p_e}$$と書き表す.これは事前に定めた定数となる(処理中に視点位置を動かす必要がないため). これで半直線の始点が分かったが,半直線を定義するためには方向ベクトルも分からなければならない.
得たい半直線は「視点位置から点(x,y)に向かう半直線」なので,方向ベクトルは視点位置から点(x,y)に向かうベクトルとなる.点(x,y)を三次元空間上の座標に変換した点の位置ベクトルを$$\overrightarrow{\bf p_w}$$とすると, 半直線の方向ベクトル$$\overrightarrow{\bf d_e}$$は以下となる(図4).
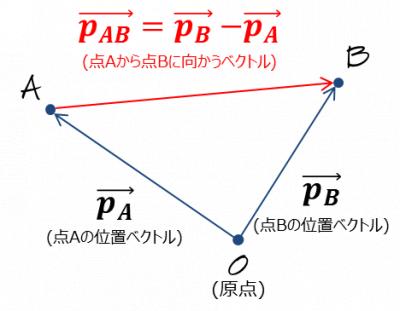
一般にある点Aからある点Bへ向かうベクトルは,位置ベクトルの引き算で表現することができる.位置ベクトルとは,空間中の位置を表す原点からその位置に向かうベクトルである.
例えば点Aの位置ベクトルを$$\overrightarrow{\bf p_A}$$,点Bの位置ベクトルを$$\overrightarrow{\bf p_B}$$, とすれば点Aからある点Bへ向かうベクトルは$$\overrightarrow{\bf p_B}-\overrightarrow{\bf p_A}$$と表現することができる(図5).
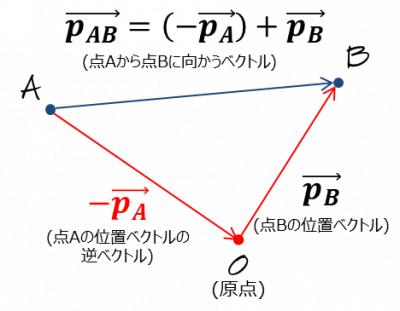
これは「ベクトルの引き算」と言うよりも,正確には$$\overrightarrow{\bf p_A}$$の逆ベクトルに$$\overrightarrow{\bf p_B}$$を加算しているといったほうが正確である(図6).
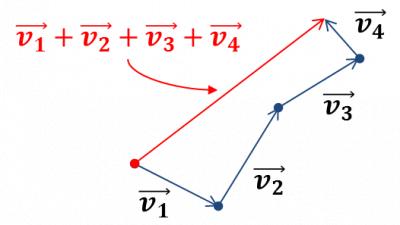
複数のベクトルの加算は,加算する全てのベクトルのうち最初のベクトルの始点から最後のベクトルの終点に向かうベクトルとなる(図7).
シーン設定
想定するシーン(視点位置や物体の位置)は以下とする(図8).
- 視点位置
- $$\vec{\bf p_{\cal e}}=(0,0,-5)$$
- スクリーン位置
- 左上$$(-1,1,0)$$, 右上$$(1,1,0)$$, 右下$$(1,-1,0)$$, 左下$$(-1,-1,0)$$
- 球
- 中心位置$$\vec{\bf p_{\cal c}}=(0,0,5)$$
- 半径$$r=1.0$$
プログラミングの前に
後述の,課題1-7 レイと球の交差判定で実際にプログラムを作り始めるが, その前にProcessingでベクトルを扱う方法を次節にて解説する.
ベクトルの扱い
ProcessingにはPVectorというベクトル計算のためのクラスが用意されている. ここではPVectorの基本的な扱い方を紹介する.
初期化
PVectorクラスのインスタンスは以下のようにして初期化する.
PVector vec1 = new PVector(); PVector vec2 = new PVector(1.0, 0.0 , 0.0);
1行目は値を指定せずに初期化している.この場合各成分は0となる.2行目はXを1, それ以外は0として初期化している.
注意:ここの説明は実験内容とは直接的には関係がないため,本当に興味があり,
かつ理解できる自信がある者だけが読むこと.
無闇に読んで頭の中を「???」でパンクさせないように気をつけること.
Processingのプログラミング言語は内部的にはJavaである.Javaはオブジェクト指向プログラミング言語という C言語とは異なるパラダイム(≒方式)のプログラミング言語である.カリキュラム的にはC言語を学んでいる人が多いはずなので, ここでオブジェクト指向プログラミングの補足説明をしておこう.
C言語ではユーザー定義型として主に構造体を用いる.ユーザー定義型とはプログラムを書く人間が
必要に応じて定義する型のことである.構造体は,intやfloatあるいはcharといった組込データ型や,
他のユーザー定義型などの複数の種類のデータを束ねたものである.
例えば,「学生」というデータに「学籍番号」「名前」「年齢」というデータが含まれているとしよう.プログラムの中でこれらのデータを扱いたいとする. C言語では以下のようになるだろうか.
int main()
{
char student_id[8]; /* 学籍番号 */
char student_name[32]; /* 名前 */
int student_age; /* 年齢 */
/* 何か処理 */
}
このままでもよいが,たとえば複数の学生を扱いたい場合はどうすればいいだろうか.1つの方法として,各データを,個別に配列に格納することが考えられる.
/* 学生数(定数) */
#define N 10
int main()
{
char student_id[N][8]; /* 学籍番号 */
char student_name[N][32]; /* 名前 */
int student_age[N]; /* 年齢 */
/* 何か処理 */
}
これでもよいが,こういった関連性の強いデータの塊は構造体として定義すると便利である.たとえば,以下のようにする.
/* 学生数(定数) */
#define N 10
/* 学生構造体 */
typedef struct {
char id[8]; /* 学籍番号 */
char name[32]; /* 名前 */
int age; /* 年齢 */
} student_t;
int main()
{
student_t students[N]; /* 学生(構造体)の配列 */
/* 何か処理 */
printf("%s\n", students[0].id); /* 0番目の学生の学籍番号を表示 */
printf("%s\n", students[0].name); /* 0番目の学生の名前を表示 */
printf("%d\n", students[0].age); /* 0番目の学生の年齢を表示 */
}
structというキーワードが構造体である.思い出してきただろうか.
JavaではC言語の構造体のようなユーザー定義型として,クラスを使用することができる.上記と等価な例をJavaで書くと以下のようになる.
final int N = 10; // 学生数(定数)
class Student
{
public char[] id; // 学籍番号
public char[] name; // 名前
public int age; // 年齢
}
Student students[] = new Student[N]; // 学生の配列
構造体の場合,内部の変数をメンバー変数とか構造体メンバーとか構造体変数とかの呼び方をするが,クラスの場合は属性という.
ちなみにC言語には文字列型のデータはなくcharの配列しかない.JavaにはStringという文字列を表すクラスが存在するため,
上記の例は以下のようにするのがより一般的である.
final int N = 10; // 学生数(定数)
class Student
{
public String id; // 学籍番号
public String name; // 名前
public int age; // 年齢
}
Student students[] = new Student[N]; // 学生の配列
このようにして定義したクラスは通常以下のようにして使用する.
Student hoge = new Student(); // 初期化 // 各データに値を代入 hoge.id = "12nc999"; hoge.name = "山田太郎"; hoge.age = 21; // 各データを表示 println(hoge.id); // 学籍番号を表示 println(hoge.name); // 名前を表示 println(hoge.age); // 年齢を表示
intやfloatなどといった組込データ型と異なり,Javaのクラスの初期化にはnewというキーワードを用いる.
これはC言語で言うと動的メモリに構造体を生成することに相当する.それ以外の各データのアクセスの仕方などは
C言語とあまり違いはない.
student_t *hoge = malloc(sizeof(student_t)); /* 初期化 */
// 各データに値を代入
strcpy(hoge->id, "12nc999");
strcpy(hoge->name, "山田太郎");
hoge->age = 21;
// 各データを表示
printf("%s\n", hoge->id);
printf("%s\n", hoge->name);
printf("%d\n", hoge->age);
free(hoge); // Javaではガベージコレクタ(≒自動メモリ管理機能)があるため不要だが
// C言語では動的メモリに確保したデータは使い終わったら解放する必要がある.
(C言語では動的メモリ上に確保したデータはポインタを通じてアクセスするので,アロー演算子(->)を使っている点に注意).
Javaではあるクラス(型)の具体的なデータ(値)をインスタンスとよぶ. 言葉がややこしいが,インスタンスとは「実例」と捉えるとわかりやすいかも知れない.
たとえば,上記の例のように「学籍番号:12nc999,名前:山田太郎,年齢:21」というデータは
Studentというクラスの実例の1つである.ほかにも「学籍番号:12nc998,名前:岩鬼正美,年齢:21」というインスタンスがあるかもしれない.
また,インスタンスのことをオブジェクトと呼ぶこともある.
ポイント
- クラスとはC言語の構造体のようなもの.
- 用語として,“クラス”は型,”インスタンス”はそのクラスの具体的な値.
- インスタンスとオブジェクトはおおよそ同義.
- Javaではクラスの初期化に
newキーワードが必要である. - クラスの中の変数(Cでいう構造体のメンバー変数)のことを属性という.
以降,必要に応じてJavaの説明を挟む.
x,y,z成分へのアクセス
PVectorクラスはx, y, z成分をあらわす(そのままの名前の)パブリックな属性を持っている.
また,setメソッドを使って一つのメソッド呼び出しでx, y, z成分を上書きすることができる.
PVector vec1 = new PVector(); vec1.x = 1.0; // x成分 vec1.y = 2.0; // y成分 vec1.z = 3.0; // z成分 vec1.set(1.0, 2.0f, 3.0); // x,y,zを一度に変更
JavaにはC言語で言う関数という概念がない.それに近い概念がメソッドである. 両者の重大な違いは,全てのメソッドは何らかのクラスに関連付いていることである.
C言語風に言うと,Javaでは構造体に関数を含めることができる,ということである.
たとえば,先ほどのStudentの例では…
class Student
{
public String id; // 学籍番号
public String name; // 名前
public int age; // 年齢
public void print() // データを表示するメソッド(≒関数)
{
println(id); // 引数がないが,上で定義されている
println(name); // 学籍番号や名前と言ったデータに
println(age); // アクセス可能である.
}
}
のようにして定義することができる.ポイントはメソッドの定義の中ではそのクラスの属性に アクセスすることができる,ということである.このようにして定義したメソッドは以下のようにして 使用することができる.
void func()
{
Student hoge = new Student();
hoge.print(); // メソッド呼び出し
}
もちろん引数付きのメソッドも定義できる.
class Student
{
// ..中略..
public int doSomething(float f){ /* ..中略.. */ }
}
ここでは余談であるが,ここまでの例やこのテキスト全体ではクラスのデータメンバー(属性)を公開状態にしている例が多いが, これはあまり適切な使い方ではない.
Javaのクラスの属性やメソッドには個別にアクセス性を設定できる.
アクセス性とは,いままでの例だと属性の前についているpublicなどのキーワードである.
class Student
{
public String id; // 学籍番号
public String name; // 名前
public int age; // 年齢
// ..中略..
}
publicと付けた属性は,クラスの外側のコードから直接アクセス(読み出し/書き込み)が可能となり,
構造体と同様の使い方ができるが,オブジェクト指向プログラミングでは通常このような使い方は推奨されない.
なぜなら,その属性の型として設定できる値が,全て正しい値であるとは限らないためである.
上記のようにクラスの属性を無秩序に書き換えができる状態にしておくと,例えば上の例なら「学生番号は空にはできない」とか 「学籍番号は『年度2桁+学科記号2-3桁+出席番号3桁』の形式」といった制限が掛けられない.
そのためデータメンバーはむき出し(public)にせず秘匿状態にするのが一般的である.Javaであれば通常publicの代わりに
privateを使用する.
class Student
{
private String id; // 学籍番号
private String name; // 名前
private int age; // 年齢
// ..中略..
}
このままではデータ(属性)に触れないので,クラスの外側のコードからそれらアクセスする必要がある場合は以下のようにする.
class Student
{
private String id; // 学籍番号
private String name; // 名前
private int age; // 年齢
// ..中略..
public String getId()
{
return id;
}
public String setId(String str)
{
if (/* str が正しい学籍番号のフォーマットである*/)
id = str;
}
}
getId/setIdメソッドを通じてデータメンバーidの読み書きをしている.このようなメソッドをアクセサメソッドという.
この講義では簡潔さを保つため,データメンバーを公開状態にしているコードが多いが製品に用いるコードなどではこのような 構成は望ましくない.
一つのポイントは,このようにして定義したメソッドはクラスのインスタンスがないと呼び出せない, と言うことである.
void func()
{
// × このような呼び出しはできない.
Student.print();
Student.doSomething(3.14);
Student hoge = new Student();
// メソッドの呼び出しにはインスタンスが必要.
hoge.print();
hoge.doSomething(3.14);
}
このように呼び出しには必ずそのクラスのインスタンスを作る必要がある. ただし,クラスのインスタンスが無くても呼び出せるメソッドも定義できる.
class Student
{
// ..中略..
public static void flyMeToTheMoon(char c){ /* ..中略.. */ }
}
メソッドの定義にstaticがつく.このようなメソッドをクラスメソッドという.以下のようにして使用する.
void func()
{
Student.flyMeToTheMoon('a'); // クラスメソッドの呼び出し
}
ちなみに,クラスメソッドに対して,先ほどのような呼び出しにクラスのインスタンスが必要な通常のメソッドを インスタンスメソッドという場合がある.
クラスメソッドは,インスタンスがなくても呼び出せるが,その定義の中ではそのクラスの属性にアクセスすることはできない. つまり,クラスの名前が頭につくだけで,実質的にC言語の関数の概念とほぼ同一のものである.
(「Processingだとクラスに関連付かないsetupやdrawを定義できるじゃないか」と思ったあなたへ.実はProcessingでは,
スケッチの実行時にスケッチ名と同名のクラスが内部的に生成されている.ProcessingではJavaやオブジェクト指向の概念を
意識しなくてもいいようにいろいろと隠されているだけである.)
ポイント
- C言語の関数≒Javaのメソッド
- Javaではクラスのメンバーとして関数を含めることができる.
- インスタンスメソッドの呼び出しには,そのクラスのインスタンスが必要.
- クラスメソッドはインスタンスがなくても呼び出すことができる.
加減算とスカラー倍
PVectorクラスにはベクトル同士の加減算,スカラー倍のためのメソッドが用意されている.
PVector.add(v1, v2)- ベクトルの加算.$$\vec{\bf v_1} + \vec{\bf v_2}$$.
PVector.sub(v1, v2)- ベクトルの減算.$$\vec{\bf v_1} – \vec{\bf v_2}$$.
PVector.mult(v, k)- ベクトルのスカラー倍.$$k\vec{\bf v}$$.
※ インスタンスメソッド版もあるが混乱を避けるためここではクラスメソッド版のみを紹介する.
以下のように行う.
PVector vec1 = new PVector(0.0f, 1.0f , 0.0f); PVector vec2 = new PVector(1.0f, 0.0f , 0.0f); PVector vec3; /* 加算 ... 意味的には vec3 ← vec1 + vec2 */ vec3 = PVector.add(vec1, vec2); /* 減算 ... 意味的には vec3 ← vec1 - vec2 */ vec3 = PVector.sub(vec1, vec2); /* スカラー倍 ... 意味的には vec3 ← 10 * vec2 */ vec3 = PVector.mult(vec2, 10);
内積,外積,ノルム(長さ)
PVectorクラスにはベクトルの内積,外積,ノルム(長さ)の計算,正規化のためのメソッドが用意されている.
v1.dot(v2)- ベクトルの内積.$$\vec{\bf v_1}\cdot\vec{\bf v_2}$$.
v1.cross(v2)- ベクトルの外積.$$\vec{\bf v_1}\times\vec{\bf v_2}$$.
v.mag()- ベクトルのノルム(長さ)の計算.$$\left|\vec{\bf v}\right|$$.
v.magSq()- ベクトルのノルム(長さ)の二乗.$$\left|\vec{\bf v}\right|^2$$.
(ノルムの計算には平方根の計算が必要だが,このメソッドは平方根の計算を省いたバージョン.こちらの方が早い場合もある.) v.normalize()- ベクトルの正規化(ノルムを1にする).$$\vec{\bf v}\leftarrow\frac{1}{\left|\vec{\bf v}\right|}\vec{\bf v}$$.
以下のように使用する.
PVector vec1 = new PVector(0.0f, 1.0f , 0.0f); PVector vec2 = new PVector(1.0f, 0.0f , 0.0f); PVector vec3; float f; // 内積 ... 意味的には f ← vec1・vec2 f = vec1.dot(vec2); // 外積 ... 意味的には vec3 ← vec1 × vec2 vec3 = vec1.cross(vec2); // ノルム(長さ) ... 意味的には f ← |vec2| f = vec2.mag(); // 正規化 ... 意味的には vec1 ← (1/|vec1|) * vec1 vec1.normalize();
ベクトルの表示
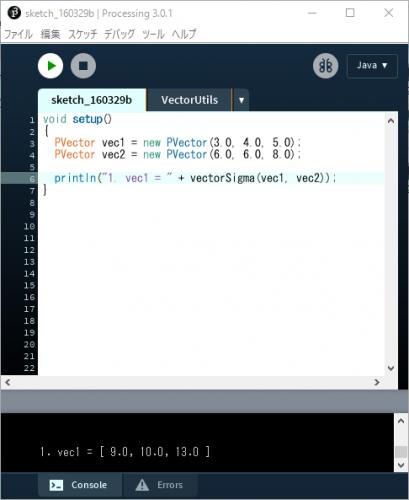
PVectorの値をprintメソッドやprintlnメソッドに渡す(正確には文字列と+演算する)と,
適当に整形してくれる.
void setup()
{
PVector vec1 = new PVector(1.0f, 2.0f, 3.0f);
print("vec1 : " + vec1);
}
結果は以下のようになる.
PVectorの利用
エイリアスに注意する
PVectorはあくまで普通のクラスであるため,PVector間の代入は参照のコピーとなることに注意せよ.
これはしばしばエイリアス(同じインスタンスを参照する複数の変数のこと)を発生させる.
例えば以下のような操作を,コーディングすることを考えてみよう.
- $$\vec{\bf v_1}\leftarrow(1.0, 2.0, 3.0)$$
- $$\vec{\bf v_1}$$を初期化
- $$\vec{\bf v_2}\leftarrow\vec{\bf v_1}$$
- $$\vec{\bf v_2}$$を$$\vec{\bf v_1}$$と同じ値で初期化
- $$\vec{\bf v_1}$$を表示
- $$\vec{\bf v_2}\leftarrow\frac{1}{\left|\vec{\bf v_2}\right|}\vec{\bf v_2}$$
- $$\vec{\bf v_2}$$を正規化
- $$\vec{\bf v_2}$$を表示
- $$\vec{\bf v_1}$$を表示
すなおにコードに落とせば以下のようになる.
PVector vec1 = new PVector(1.0, 2.0, 3.0);
PVector vec2 = vec1; // vec2にvec1をコピー(したつもり)
println("vec1 : " + vec1); // vec1の内容を表示
vec2.normalize(); // vec2を正規化する
print("vec2 : " + vec2); // vec2の内容を表示
print("vec1 : " + vec1); // 再びvec1の内容を表示
これは以下のような結果となる.
この出力の1行目と3行目に注目しよう.
これらはコードの5行目と11行目に対応する.
PVector vec1 = new PVector(1.0, 2.0, 3.0);
PVector vec2 = vec1; // vec2にvec1をコピー(したつもり)
println("vec1 : " + vec1); // vec1の内容を表示
vec2.normalize(); // vec2を正規化する
print("vec2 : " + vec2); // vec2の内容を表示
print("vec1 : " + vec1); // 再びvec1の内容を表示
この二つの行の間ではvec1の値に何か影響を与える操作はしていないはずである.この間にvec2を正規化しているが,
別の変数であるvec1も値が変わってしまった,ように見える.これは以下のような理由による.
まず,1行目でPVectorの新たなインスタンスを生成(new)し,vec1はこのインスタンスを指している状態となる.
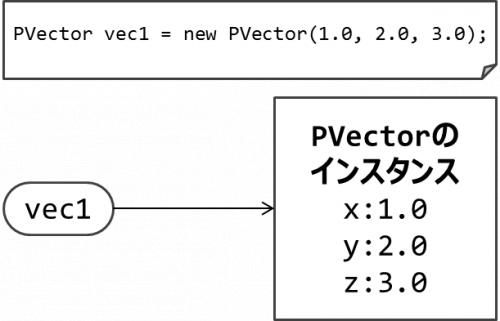
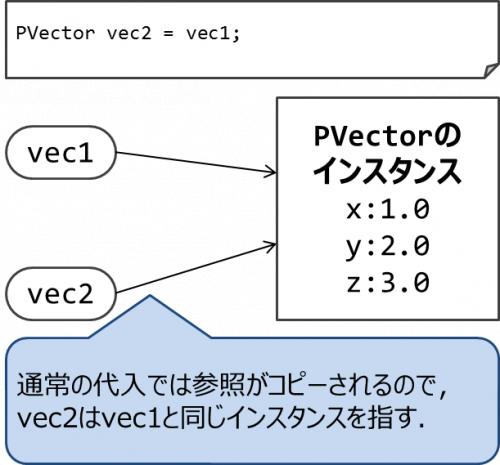
次に,3行目でvec1の内容をvec2にコピーするつもりで代入を行っている.この代入は実際には
PVectorのインスタンスをコピーするわけではなく,vec2がvec1と同じインスタンスを指すように変更してしまう.
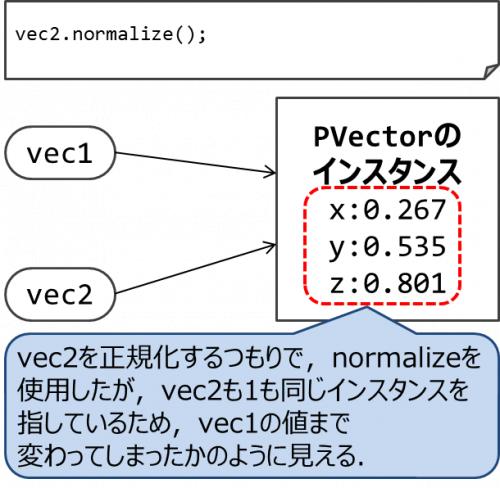
そして,6行目ではvec2を正規化しているつもりだが,vec2とvec1は同じ場所を指しているので,
結果的にvec1の値が変わったかのように見えてしまう.
このように,PVectorを通常のプリミティブ型(intやfloatなど)であるかのように扱うと思わぬ結果を招く場合があるため注意する必要がある.
インスタンスをコピーしたい場合はcopyメソッドを使う必要がある.
PVector vec1 = new PVector(1.0, 2.0, 3.0);
PVector vec2 = vec1.copy(); // vec2にvec1をコピー
print("vec1 : " + vec1); // vec1の内容を表示
vec2.normalize(); // vec2を正規化する
print("vec2 : " + vec2); // vec2の内容を表示
print("vec1 : " + vec1); // 再びvec1の内容を表示
これで意図通りに動作する.
このエイリアスの問題というのは,要するに複数のポインタ型の変数が同じメモリを指している,ということである. Javaのクラスのインスタンスは常に動的メモリに作られる.C言語に置き換えてみれば,上記は以下と同じことをしていることになる.
PVector *vec1 = malloc(sizeof(PVector)); PVector *vec2 = vec1; /* vec2にvec1をコピー(したつもり) */ /* ..中略.. */
1行目で,vec1はmalloc関数で確保したメモリを指すようになり,3行目でvec2も同じメモリを指してしまう,ということである.
確保したPVectorのメモリ上の実体は1つなので,vec1を通じて操作してもvec2を通じて操作しても同じ実体の値を書き換えてしまうことになる.
インスタンスのコピーとは,同じ値を持つ実体をもう一つ作る,ということである.つまりcopyメソッドは以下と等価なことをしている.
PVector *vec1 = malloc(sizeof(PVector)); PVector *vec2 = malloc(sizeof(PVector)); /* copyメソッドはこの2行と */ memcpy(vec2, vec1, sizeof(PVector)); /* 同じことをしている. */ /* ..中略.. */
ベクトル計算の簡略化
PVectorはあくまで普通のクラスであるため,通常のプリミティブ型のように
中置記法の計算式を書くことができない.これは計算過程の中間結果を保持するために,一時変数を用意することがある必要があることを意味する.
例えば以下の計算式を
PVectorを用いて表すと以下のようになる.
PVector vec1 = /* 何らかの値 */; PVector vec2 = /* 何らかの値 */; PVector vec3; // こうは書けないので… vec3 = 5 * vec1 + 10 * vec2; // 一時変数1 PVector tmp1 = PVector.mult(vec1, 5); // +演算子の左側を計算して保存 // 一時変数2 PVector tmp2 = PVector.mult(vec2, 10); // +演算子の右側を計算して保存 vec3 = PVector.add(tmp1, tmp2); // ようやく所期の計算ができる
これは大変不便である.
本実験では二つのベクトルの加減算をいたるところで使用するための,いちいち一時変数を用意していると
ソースが大変煩雑なものとなる.
一時変数を用いずに書くことも可能ではあるが…
PVector vec1 = /* 何らかの値 */; PVector vec2 = /* 何らかの値 */; PVector vec3; vec3 = PVector.add(PVector.mult(vec1, 5), PVector.mult(vec2, 10));
上記程度であればまだ読めなくはないが,以下のようなより複雑な計算の場合には…
PVector vec1 = /* 何らかの値 */; PVector vec2 = /* 何らかの値 */; PVector vec3 = /* 何らかの値 */; PVector vec4; vec4 = PVector.add(PVector.sub(PVector.mult(vec1, 5), PVector.mult(vec2, 3)), PVector.mult(vec3, 10));
やはり大変煩雑となるし,このコードを見てどのようなベクトル計算を意図したものなのかを 読み取るのは難しい.
そこでベクトルの線形和$$\left(\sum{k_i\vec{\bf v_i}}\right)$$を計算するメソッドvectorSigmaを用意しておこう.セットアップ方法は後述する.
使い方は単純で,引数としてスカラーとベクトルを交互に渡せば良い.
float k1, k2, k3; // ここでは省略しているが, PVector vec1, vec2, vec3; // もちろん適切に初期化しておく必要がある. PVector vec4 = vectorSigma(k1, vec1, k2, vec2, k3, vec3); // 線形和を計算してvec4に代入
上記の例なら要素3のスカラーの集合$$k=\lbrace k_1, k_2, k_3 \rbrace $$と,同じく要素3のベクトルの集合$$v=\lbrace \vec{\bf v_1}, \vec{\bf v_2}, \vec{\bf v_3} \rbrace$$を使って,
を計算してくれる.なお要素は3つに限らずいくつでも渡すことができる.
Processing(Java)でも,C言語と同様に可変長引数のメソッドを定義することができる.
vectorSigmaは引数をすべてObject型の配列として受け取るメソッドである.
PVector vectorSigma(Object ... params)
{
PVector result = new PVector(0,0,0);
for(int i = 0; i < params.length;)
{
if ( params[i] instanceof Number )
{
if ( i+1 > params.length-1 || !(params[i+1] instanceof PVector) )
throw new IllegalArgumentException();
float k = ((Number)params[i]).floatValue();
PVector v = (PVector)params[i+1];
result.add(PVector.mult(v, k));
i += 2;
}
else if ( params[i] instanceof PVector )
{
PVector v = (PVector)params[i];
result.add(v);
++i;
}
}//for
return result;
}
ループの中で引数に渡された配列の型をチェック(instanceof)して線形和の動作を実現している.
(C言語ではこれと同じものは実現不可能である.なぜなら,このメソッドは実行時型情報(メモリブロックに何の型のデータが入っているかを示す情報)を利用しているためである.)
以下のようにして使う.以下の計算式(一つ目の例)ならば,
以下のように書ける.
PVector vec1 = /* 何らかの値 */; PVector vec2 = /* 何らかの値 */; PVector vec3 = vectorSigma(5, vec1, +10, vec2);
引数として,スカラー(float)とPVectorのインスタンスを交互に渡している点がポイントである.
ただし係数が不要な場合は省略が可能である.例えば以下のような計算の場合は,
次のように表現できる.
PVector vec1 = /* 何らかの値 */; PVector vec2 = /* 何らかの値 */; PVector vec3 = vectorSigma(5, vec1, vec2);
さらに,負数を係数として使用すれば減算も表現可能である.例えば,以下の式ならば,
PVector vec1 = /* 何らかの値 */; PVector vec2 = /* 何らかの値 */; PVector vec3 = vectorSigma(5, vec1, -1, vec2);
また,以下の先ほどの複雑な計算も一つのメソッド呼び出しで実現できる.
PVector vec1 = /* 何らかの値 */; PVector vec2 = /* 何らかの値 */; PVector vec3 = /* 何らかの値 */; PVector vec4 = vectorSigma(5, vec1, -3, vec2, +10, vec3);
準備作業の追加
上記で紹介したvectorSigmaメソッドを直接スケッチに描き込んでもよいが,
見通しが悪くなるためソースコードを分けよう.以下のようにする.
C.1) 新たなスケッチを作って保存を済ませたと仮定する.
C.2) タブの隣の下向きの三角形(▼)をクリックし,新規タブを選択する.
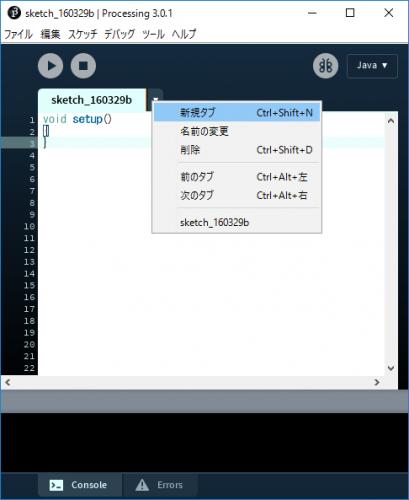
C.3) ファイル名の入力を求められる(画面下部)ので,適当な名前を入力する.ここではVectorUtilsと入力してOKボタンをクリックする.
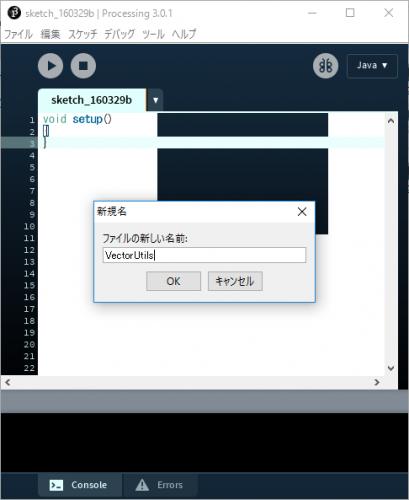
C.4) 空のタブがスケッチに追加される.
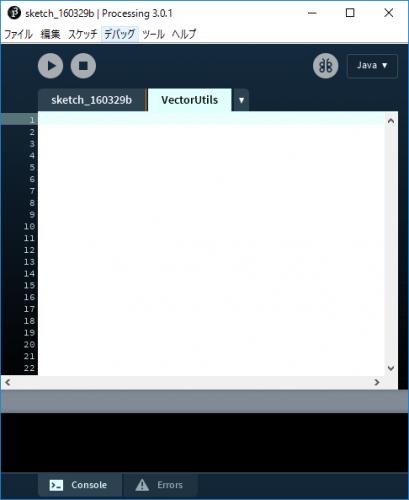
C.5) 以下のボタンを押すと必要なソースコードがコピーされるので,C.4の空のタブ(VectorUtils)にペーストする.
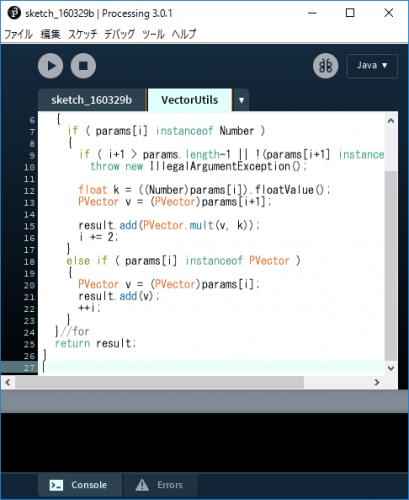
C.6) 以上でメイン側のソースファイルでVectorUtils側のメソッドが使用できるようになる.この状態で一度保存しておこう.
課題
課題1-6 ベクトルを扱う練習
(作業時間目安:10分)
※ この課題に取り組む前に,このページの「ベクトルの扱い」 「PVectorの利用」をよく読むこと.
3つのベクトル$$\vec{\bf v_1}, \vec{\bf v_2}, \vec{\bf v_3}$$を定義し,これらを使った以下の計算結果を 表示するスケッチを作成せよ.このスケッチはVectorTestという名前で保存せよ.
$$\vec{\bf v_1}, \vec{\bf v_2}, \vec{\bf v_3}$$の初期値は以下である.
以下の順序で処理を行え.
- $$\vec{\bf v_1}$$の値を表示する.
- $$\vec{\bf v_2}$$の値を表示する.
- $$\vec{\bf v_3}$$の値を表示する.
- $$\vec{\bf v_1} + \vec{\bf v_2}$$を計算し,その結果を表示する.
- $$3\vec{\bf v_1} + 4\vec{\bf v_2}$$を計算し,その結果を表示する.
- $$\vec{\bf v_3}$$のベクトルを$$\vec{\bf v_1}$$にコピーし,$$\vec{\bf v_1}$$の値を表示する.
- $$\vec{\bf v_1}$$のY成分に0を代入し,その結果を表示する.
- $$2\vec{\bf v_1} – 5\vec{\bf v_2} + 10\vec{\bf v_3}$$を計算し,その結果を表示する.
- $$\vec{\bf v_2}\cdot\vec{\bf v_3}$$を計算し,その結果を表示する.
- この計算式はベクトルの内積である.ベクトルの内積の計算結果はスカラーであることに留意すること.
- $$\vec{\bf v_2}\times\vec{\bf v_3}$$を計算し,その結果を表示する.
- この計算式はベクトルの外積である.ベクトルの外積の計算結果はベクトルであることに留意すること.
※ このスケッチはコンソールへの出力のみを行うため,setupの中に全ての処理を詰め込んでもよい.
また,このスケッチは描画を行わないため,drawメソッドを定義する必要はない.
なお以下の実行結果のように行頭に番号を振って出力せよ.
ヒント1
課題1-7 レイと球の交差判定
(作業時間目安:40分)
「最初の実装」で示したレイと球の交差判定を行うスケッチを作成せよ.
レイと球が交差する場合は赤を出力し,交差しない場合は青を出力すること.
シーンの設定は「シーン設定」に従う.
このスケッチはFirstSampleという名前で保存せよ.
画像サイズは幅512ピクセル,高さ512ピクセルとせよ.
生成画像は図9のようになる.

図9. FirstSampleの生成画像
ヒント1
ヒント2
- 全ての補足問題に取り組む必要はありません.十分にヒントが得られたと思ったら本題に引き返しましょう.
- 作業時間は限られているので,この補足問題を参考にして0からコードを書くか,この次のヒント(日本語で書き下したコード)や 次の次のヒント(穴埋め)を使うかは自分の実力とよく相談して下さい.
ヒント3
- $$W,H$$
- 画像の幅と高さ
- $$\overrightarrow{\bf p_e}$$
- 視点位置
- $$\overrightarrow{\bf p_c}$$
- 球の中心位置
- $$r$$
- 球の半径
- $$\overrightarrow{\bf p_w}$$
- スクリーン上の点の位置.$$\overrightarrow{\bf p_w} = (x_w, y_w, 0)$$.
- スクリーン座標$$y_s$$を$$[0,H)$$の範囲でループする.
- スクリーン座標$$y_s$$を三次元空間座標$$y_{w}$$に変換する.
- $$y_w = \frac{-2y_s}{H-1}+1.0$$
- スクリーン座標$$x_s$$を$$[0,W)$$の範囲でループする.
- スクリーン座標$$x_s$$を三次元空間座標$$x_{w}$$に変換する.
- $$x_w = \frac{2x_s}{W-1}-1.0$$
- 視線ベクトル$$\vec{\bf d_{\cal e}}$$を計算する.
- $$\vec{\bf d_{\cal e}}=\vec{\bf p_{\cal w}}-\vec{\bf p_{\cal e}}$$
- 交点計算で必要なので,$$\overrightarrow{\bf v_{\cal tmp}}=\vec{\bf p_{\cal e}}-\vec{\bf p_{\cal c}}$$を計算しておく.
- 交点計算のため二次方程式$$At^{2}+Bt+C=0$$の係数$$A,B,C$$を計算する.
- $$A=\left|\vec{\bf d_{\cal e}}\right|^{2}$$
- $$B=2\left(\vec{\bf d_{\cal e}}\cdot\overrightarrow{\bf v_{\cal tmp}}\right)$$
- $$C=\left|\overrightarrow{\bf v_{\cal tmp}}\right|^{2}-r^{2}$$
- 判別式$$D$$の値を計算する.
- $$D=B^{2}-4AC$$
- $$D\ge0$$のとき
- 赤$$RGB=(255,0,0)$$を出力
- それ以外のとき
- 青$$RGB=(0,0,255)$$を出力
- スクリーン座標$$x_s$$を三次元空間座標$$x_{w}$$に変換する.
- スクリーン座標$$y_s$$を三次元空間座標$$y_{w}$$に変換する.
ヒント4
ヒント5
// 定数の初期化
PVector eyePos = /* 穴埋め1 */; // 視点位置
PVector spherePos = /* 穴埋め2 */; // 球の中心位置
float sphereR = /* 穴埋め3 */; // 球の半径
void setup()
{
size(512, 512);
background(color(0,0,0));
noSmooth();
noLoop();
}// void setup()
void draw()
{
PVector pw = new PVector();
pw.z = 0;
for(int y = 0; y < height; ++y)
{
pw.y = /* 穴埋め4 */;
for(int x = 0; x < width; ++x)
{
pw.x = /* 穴埋め5 */;
PVector eyeDir = /* 穴埋め6 */; // 視線方向
PVector tmp = /* 穴埋め7 */; // 視点 - 球の中心
// 二次方程式の係数(At^2 + Bt + C = 0)
float A = /* 穴埋め8 */;
float B = /* 穴埋め9 */;
float C = /* 穴埋め10 */;
float D = /* 穴埋め11 */; // 判別式
if(/* 穴埋め12 */)
stroke(color(255,0,0));
else
stroke(color(0,0,255));
point(x, y);
}//for
}//for
}// void draw()
0 Comments.