課題1-7補足問題
ここの問題は課題1-7 レイと球の交差判定
が難しいと感じたら取り組んでください.
十分にヒントを得られたと思ったら,途中でやめて「課題1-7 レイと球の交差判定」に戻っても構いません.
シーン設定
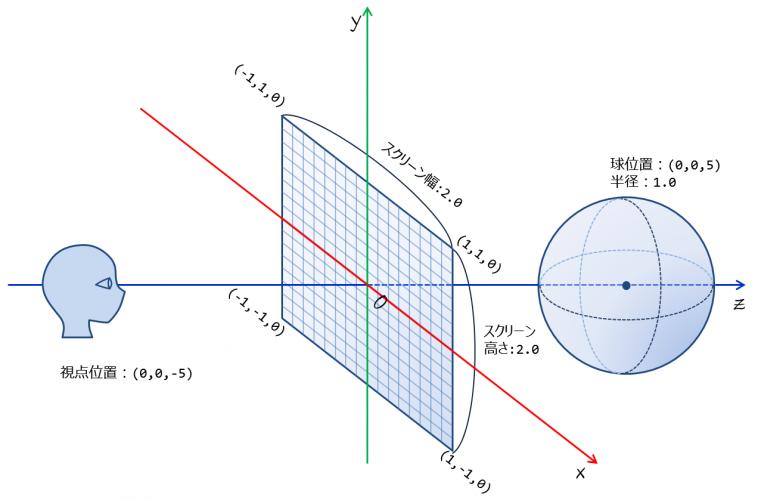
「課題1-7 レイと球の交差判定」で想定しているシーンを再掲する.
- 視点位置
- $$\vec{\bf p_{\cal e}}=(0,0,-5)$$
- スクリーン位置
- 左上$$(-1,1,0)$$, 右上$$(1,1,0)$$, 右下$$(1,-1,0)$$, 左下$$(-1,-1,0)$$
- 球
- 中心位置$$\vec{\bf p_{\cal c}}=(0,0,5)$$
- 半径$$r=1.0$$
補足問題1
スクリーン座標$$(382,255)$$を,三次元空間上の座標に変換するスケッチを作成せよ. このスケッチはOneConvという名前で保存せよ.
変換方法は「スクリーン座標の変換」の通りである. 変換式を以下に再掲する.
void setup()
{
size(512, 512);
// スクリーン座標
int x = 382;
int y = 255;
PVector pw = new PVector();
pw.x = /* 穴埋め1 */;
pw.y = /* 穴埋め2 */;
pw.z = /* 穴埋め3 */;
println("(" + x + ", " + y + ") -> " + pw);
}結果は以下のようになるはずである.
ヒント1
まず,手計算できるかどうか試してみよ.
ヒント2
数値の型と,その除算の振る舞いに注意する.
たとえば,自然な考えでは,$$1 \div 2$$の結果は$$0.5$$となる.しかし,プログラミングでは必ずしもそうはならない.
void setup()
{
float hoge = 1 / 2;
println(hoge);
}
この結果は以下のようになる.
$$1 \div 2$$の結果がゼロになってしまった.なぜだろうか?
ヒント3
Processing(Java)では,整数同士の除算の結果は整数となる.
整数 / 整数 → 整数
$$1 \div 2$$の計算結果は,本来は$$0.5$$となりそうだが,前掲したコードでは被除数は1,除数は2というリテラル(定数)で表現されている.
void setup()
{
float hoge = 1 / 2;
println(hoge);
}
ソースコード中に単に1や2と書いた場合は,その数は整数型であるとして解釈される.したがって計算結果は$$0.5$$が整数に丸められて0となる.
これを回避するには演算子のオペランドの少なくとも一方が実数型であれば良い.
演算子とはこの場合/のことであり,オペランド(被演算子)とは1と2のことである.
Javaでは演算子のオペランドの型が異なる場合,演算の前に型の昇格が発生する. 型の昇格とは,二つのオペランドのうち大きい方の型にもう一方の型も合わせられる,ということである.
たとえば,以下のような整数と実数の計算の場合,
実数 / 整数
計算の前に,整数は実数に昇格されて実数になる.実数同士の除算は実数となる.
実数 / 実数 → 実数
型の大きさの順序としては,おおよそdouble > float > long > intという順序である.
先ほどの例ならば.
void setup()
{
float hoge = 1.0f / 2;
println(hoge);
}
と書くと,/演算子の両側が実数(float)として解釈され,計算結果は所期の0.5となる.
Javaでは(Cでもおおよそ同じ仕様だが),数値の書き方によってその数値がいかなる型として解釈されるかが変わってくる. 例えば$$1$$ならば,ソースコード中の書き方によって以下のように解釈される(参考1,参考2).
| リテラル | 型 |
|---|---|
1 | int |
1L | long |
1.0f | float |
1.0 | double |
1.0d |
前述の例では,一方のオペランドを1.0fと記述したため,昇格が起きて二つ目のオペランド2が整数型から実数型に格上げされた.
リテラルの場合は,上記のようにすれば良いが変数同士の演算の場合にはどうすればよいか?
void setup()
{
int foo = 1;
int bar = 2;
float hoge = foo / bar;
println(hoge);
}
この結果は最初と同じく0に丸められてしまう./演算子のオペランドとして与えられている式fooもbarも整数型であるためである.
このような場合はキャストを使えばよい.
キャストとは値を(可能な範囲で)強制的に別の型に変換する記法である.キャストは,型変換したい式の前に(型名)をつける.
例えば上記の例であれば.
void setup()
{
int foo = 1;
int bar = 2;
float hoge = (float)foo / bar;
println(hoge);
}
式fooの前に(float)と付けている.これによって/演算子の一方が実数として解釈され,演算結果も実数となる.
ちなみに演算子のとどちらか一方が実数であればいいので以下でも同じである.
void setup()
{
int foo = 1;
int bar = 2;
float hoge = foo / (float)bar;
println(hoge);
}
念のため,以下のようにするとうまくいかない.
void setup()
{
int foo = 1;
int bar = 2;
float hoge = (float)(foo / bar);
println(hoge);
}
キャストは個々の変数やリテラルに対して作用する,というよりもそれらと演算子の組合せである式に対して作用する.
上記の例ではキャストの適用先はfooでもbarでもなく(foo / bar)である.これは整数 / 整数であるため,
式の値は0となる.
つまり(float)(foo / bar)は(float)(0)としているのと同じであるため意味が無い.
このようにプログラミングにおける除算では,/演算子のオペランドの型に注意する必要がある.
補足問題2
視点$$\vec{\bf p_{\cal e}} = (0,0,-5)$$から,スクリーン上の点$$\vec{\bf p_{\cal w}}=(-0.4, 0, 0)$$への半直線は球と交点を持つかどうか判定するスケッチを作成せよ.交差する場合は「Yes!」,しない場合は「No…」とコンソールに表示すること.
このスケッチはOneSampleという名前で保存すること.
void setup()
{
size(512, 512);
PVector eyePos = new PVector( 0, 0, -5 ); // 視点位置
PVector spherePos = new PVector( 0, 0, 5 ); // 球の中心
float sphereR = 1.0; // 球の半径
PVector pw = new PVector( -0.4, 0, 0 ); // スクリーン上の点
PVector eyeDir = /* 穴埋め1 */; // 視線方向
PVector tmp = /* 穴埋め2 */; // 視点 - 球の中心
// 二次方程式の係数(At^2 + Bt + C = 0)
float A = /* 穴埋め3 */;
float B = /* 穴埋め4 */;
float C = /* 穴埋め5 */;
float D = /* 穴埋め6 */; // 判別式
if ( /* 穴埋め7 */ )
println("Yes!");
else
println("No...");
}
結果は交差するはずである(視点と球の位置関係を思い浮かべてみよう).
ヒント1
キーボードから手を離せ!話はそれからだ!!
- 「理屈」を理解することなしにコードは書けない.
- 「交点の有無を調べる方法」を理解しているかどうか自分に問いただしてみよ.
- それを自分の言葉で説明できないうちは,まだ「理屈」を理解していない.
- 「理屈」の理解をなしにして,テキストエディタを開きキーボードに手を置いたところで全くの無駄である.まずは「理屈」の理解に努めよ.
これは数学の問題である.設問を再掲する.
問
位置$$\overrightarrow{\bf p_e} = (0,0,-5)$$から,位置$$\overrightarrow{\bf p_w}=(-0.4, 0, 0)$$へ向かう半直線は,中心位置$$\overrightarrow{\bf p_c} = (0,0,5)$$,半径$$r=1$$の球と交点を持つかどうか.
理屈
- tの方程式,$$At^2+Bt+C=0$$の係数$$A$$,$$B$$,$$C$$がわかれば,交差の有無を調べることができる.
- その方法は,判別式$$D=B^2-4AC$$の値が正の数かゼロか負の数かを調べることである.
以下を試みよ.
- まず,プログラミングとは関係なしに,ノートと手計算を駆使して交差の有無を調べよ.
ヒント2
以下のことを検討せよ.
- 係数$$A$$,$$B$$,$$C$$を計算するために必要なベクトルをすべて洗い出せ.
- 必要なベクトルを全てノートに書き出せ.必要ならば適切な名前や記号を付けよ.
- 洗い出したベクトルそれぞれについて以下のことを調べよ.
- 【Q1】そのベクトルを格納するために必要な変数が,穴埋めコードの中にあるかどうか?(ある/ない)
- 【Q2】その変数にはすでに必要な値が代入されているか?(いる/いない)
- 【Q3】必要な値が代入されていない場合,それを代入することは可能か.以下の項目を調べよ.
- 【Q3-1】その値を計算するための数式を書き出せ(コードではなく,数式で).
- 【Q3-2】その数式の値を計算するのに必要な値はそろっているか?(そろっている/そろっていない)
- 【Q3-3】計算に必要な値は,穴埋めコードの中のどこに当たるか.
- 【Q3-4】Q3-1で検討した数式を,コードで書き表すことはできるか?
ヒント3
穴埋めの位置ですべきこと
- 穴埋め1
- $$\vec{\bf d_{\cal e}}$$を計算する.
- 穴埋め2
- $$\vec{\bf m}$$を計算する.
- 穴埋め3
- 係数Aの値を計算する.
- 穴埋め4
- 係数Bの値を計算する.
- 穴埋め5
- 係数Cの値を計算する.
- 穴埋め6
- 判別式Dの値を計算する.
- 穴埋め7
- 判別式Dの値から,交点を持つ条件を書く.
凡例
- $$\vec{\bf c}$$
- 球の中心点$${\cal c}$$の位置ベクトル
- $$r$$
- 球の半径
- $$\vec{\bf p_{\cal e}}$$
- 視点の位置ベクトル
- $$\vec{\bf p_{\cal w}}$$
- スクリーン上の点$${\cal p_{w}}$$の位置ベクトル
- $$\vec{\bf d_{\cal e}}$$
- 視線ベクトル
- $$\vec{\bf m}$$
- $$\vec{\bf p_{\cal e}}$$から$$\vec{\bf c}$$を引いたベクトル
ヒント4
$$\leftarrow$$は代入を表す.
- 穴埋め1
- $$\vec{\bf d_{\cal e}}\leftarrow\vec{\bf p_{\cal w}}-\vec{\bf p_{\cal e}}$$
- 穴埋め2
- $$\vec{\bf m}\leftarrow\vec{\bf p_{\cal e}}-\vec{\bf c}$$
- 穴埋め3
- $$A\leftarrow\left|\vec{\bf d_{\cal e}}\right|^{2}$$
- あるいは$$A\leftarrow\vec{\bf d_{\cal e}}\cdot\vec{\bf d_{\cal e}}$$
- $$A\leftarrow\left|\vec{\bf d_{\cal e}}\right|^{2}$$
- 穴埋め4
- $$B\leftarrow2\left(\vec{\bf d_{\cal e}}\cdot\vec{\bf m}\right)$$
- 穴埋め5
- $$C\leftarrow\left|\vec{\bf m}\right|^{2}-r^{2}$$
- あるいは$$C\leftarrow\left(\vec{\bf m}\cdot\vec{\bf m}\right)-r^{2}$$
- $$C\leftarrow\left|\vec{\bf m}\right|^{2}-r^{2}$$
- 穴埋め6
- $$D\leftarrow B^2-4AC$$
- 穴埋め7
- $$D\geq0$$
ヒント5
- $$\vec{\bf c}$$
- 変数spherePos(PVector型)
- $$r$$
- 変数sphereR(float型)
- $$\vec{\bf p_{\cal e}}$$
- 変数eyePos(PVector型)
- $$\vec{\bf p_{\cal w}}$$
- 変数pw(PVector型)
- $$\vec{\bf d_{\cal e}}$$
- 変数eyeDir(PVector型)
- $$\vec{\bf m}$$
- 変数tmp(PVector型)
補足問題3
スクリーン座標$$(382,255)$$を三次元空間上の座標$$\vec{\bf p_{\cal w}}$$に変換し,さらに視点から$$\vec{\bf p_{\cal w}}$$への 半直線が球と交差するかどうかを判定するスケッチを作成せよ.交差する場合は「Yes!」,しない場合は「No…」と表示すること.
このスケッチはOneConvSampleという名前で保存すること.
(穴埋めソースは掲載しない.補足問題1および2を応用すれば作ることができる.)
結果は交差するはずである.
補足問題4
全てのスクリーン座標$$p_s=(x_s,y_s)$$を,三次元空間上の座標$$\overrightarrow{\bf p_w}$$に 変換してコンソールに出力するスケッチを作成せよ.
このスケッチはAllConvという名前で保存せよ.
(穴埋めソースは掲載しない.補足問題1および「課題1-1 塗りつぶし(復習)」を応用すれば作ることができる.)
本来のスクリーンのサイズは、幅512ピクセル,高さ512ピクセルであるが,このスケッチでは コンソールの出力量が多いため,幅10ピクセル,高さ10ピクセルとする.
結果は以下のようになる.
補足問題5
全てのスクリーン座標$$p_s=(x_s,y_s)$$を,三次元空間上の座標$$\overrightarrow{\bf p_w}$$に 変換して,視点位置$$\overrightarrow{\bf p_e}=(0,0,-5)$$から$$\overrightarrow{\bf p_w}$$を 通る半直線が球と交点を持つかどうかを調べるスケッチを作成せよ.
交差があった場合,その点のスクリーン座標とそれに対応する三次元座標を表示すること. 交差がなかった場合は,なにも表示しない.
このスケッチはAllSampleという名前で保存すること.
補足問題4と同様,このスケッチではコンソールの出力量が多いため, スクリーンの幅を幅10ピクセル,高さ10ピクセルとする.
void setup()
{
size(10, 10);
PVector eyePos = new PVector( 0, 0, -5 ); // 視点位置
PVector spherePos = new PVector( 0, 0, 5 ); // 球の中心
float sphereR = 1; // 球の半径
PVector pw = new PVector(); // スクリーン上の点
pw.z = /* 穴埋め1 */;
for(int y = 0; y < height; ++y)
{
pw.y = /* 穴埋め2 */;
for(int x = 0; x < width; ++x)
{
pw.x = /* 穴埋め3 */;
PVector eyeDir = /* 穴埋め4 */; // 視線方向ベクトル
PVector tmp = /* 穴埋め5 */; // 視点 - 球の中心
// 二次方程式の係数(At^2 + Bt + C = 0)
float A = /* 穴埋め6 */;
float B = /* 穴埋め7 */;
float C = /* 穴埋め8 */;
float D = /* 穴埋め9 */; // 判別式
if ( /* 穴埋め10 */ )
println("(" + x + ", " + y + ") -> " + pw);
}// for
}// for
}// void setup()
結果は以下のようになる.
0 Comments.